Để học tốt Hình Học 10, phần dưới giải các bài tập sách giáo khoa Toán 10 được biên soạn bám sát theo nội dung SGK Toán Hình Học 10. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Tích Của Vectơ Với Một Số – Toán 10 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!

I. Lý thuyết Tích của vectơ với một số

1. Định nghĩa

Cho số k ≠ 0 và vectơ Tích của vectơ với số k là một vectơ, kí hiệu là k , cùng hướng với nếu k > 0, ngược hướng với nếu k < 0 và có độ dài bằng |k|.||

2. Tính chất

Với hai vectơ  bất kì, với mọi số h và k, ta có

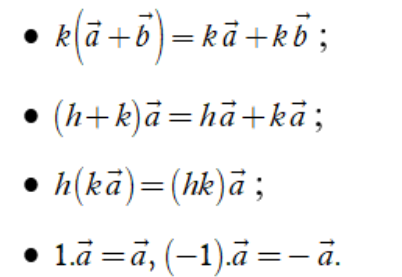
3. Trung điểm của đoạn thẳng và trọng tâm của tam giác

a) Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M thì ta có

b) Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M thì ta có

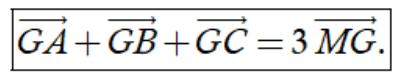
4. Điều kiện để hai vectơ cùng phương

Điều kiện cần và đủ để hai vectơ  cùng phương là có một số k để

Nhận xét. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để

5. Phân tích một vectơ theo hai vectơ không cùng phương

Cho hai vectơ không cùng phương. Khi đó mọi vectơ  đều phân tích được một cách duy nhất theo hai vectơ nghĩa là có duy nhất cặp số h, k sao cho

II. GIẢI BÀI TẬP SGK

Bài 1 (trang 17 SGK Hình học 10):

Cho hình bình hành ABCD. Chứng minh rằng:

Lời giải:

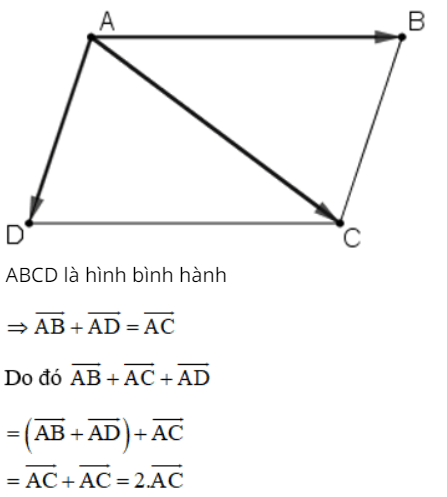
Bài 2 (trang 17 SGK Hình học 10):

Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ theo hai vec tơ

Lời giải:

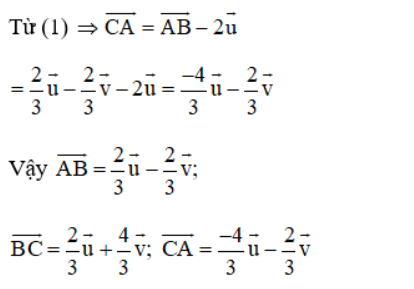
Bài 3 (trang 17 SGK Hình học 10):

Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho . Hãy phân tích vec tơ theo hai vec tơ

Lời giải:

Bài 4 (trang 17 SGK Hình học 10):

Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM.

Chứng minh rằng:

Lời giải:

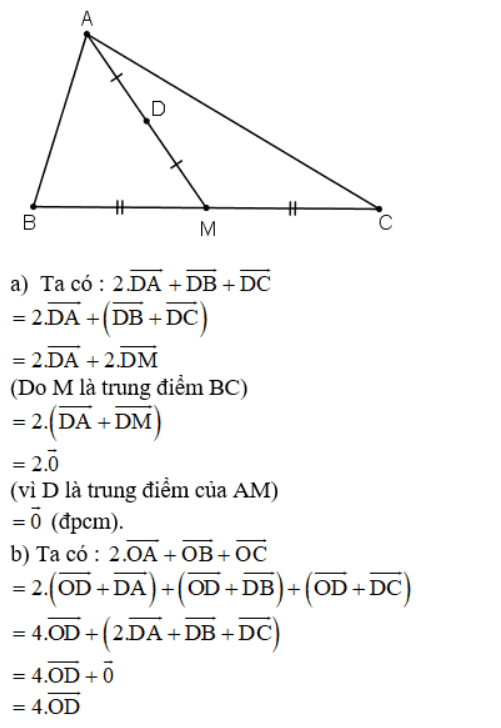
Bài 5 (trang 17 SGK Hình học 10):

Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD.

Chứng minh rằng:

Lời giải:

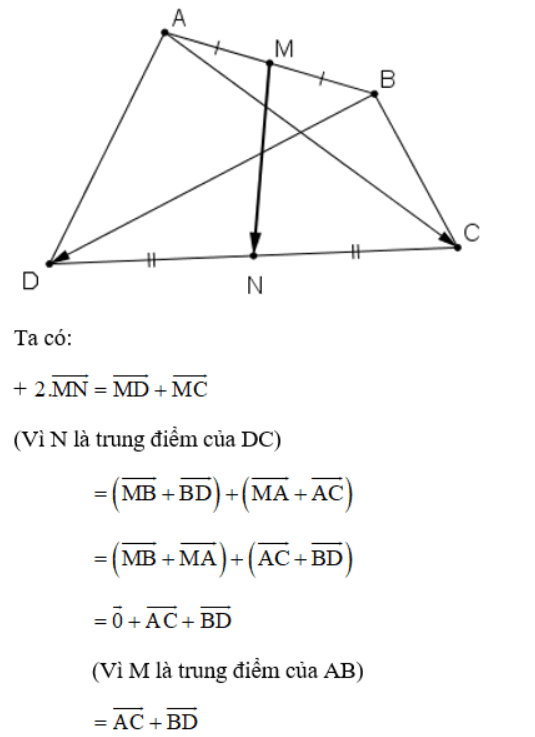
Bài 6 (trang 17 SGK Hình học 10):

Cho hai điểm phân biệt A và B. Tìm điểm K sao cho

Lời giải:

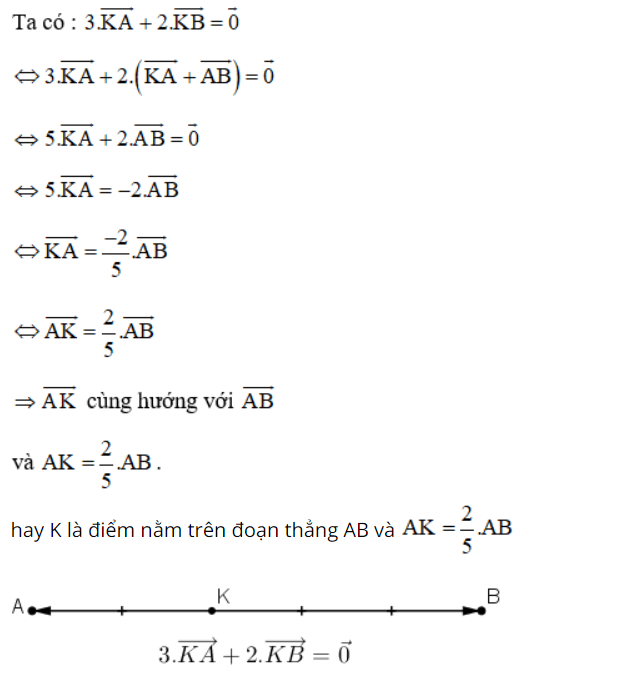
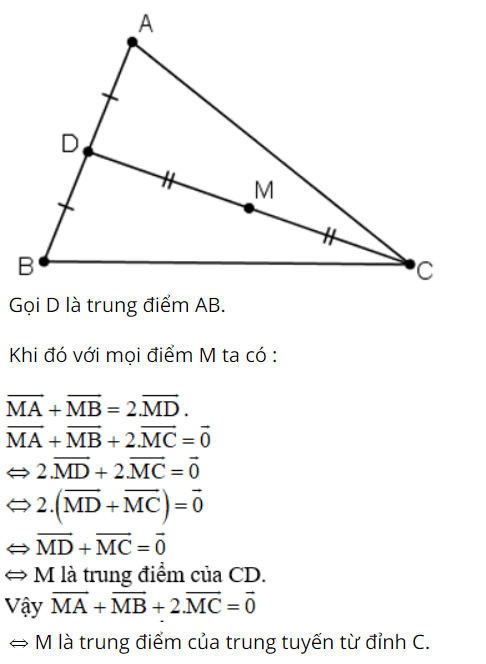
Bài 7 (trang 17 SGK Hình học 10):

Cho tam giác ABC. Tìm điểm M sao cho

Lời giải:

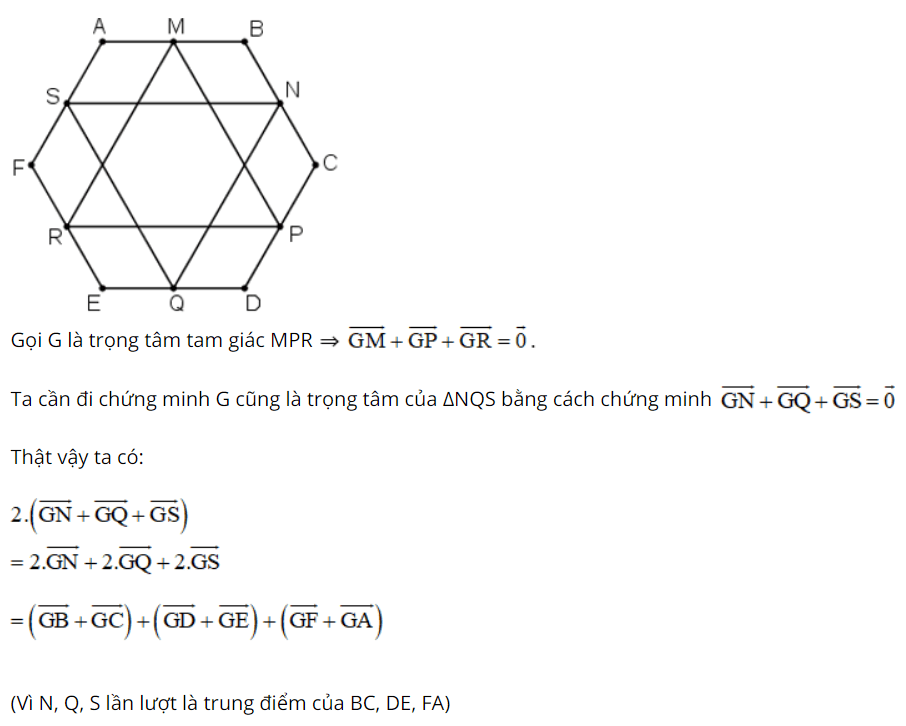
Bài 8 (trang 17 SGK Hình học 10):

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Lời giải:

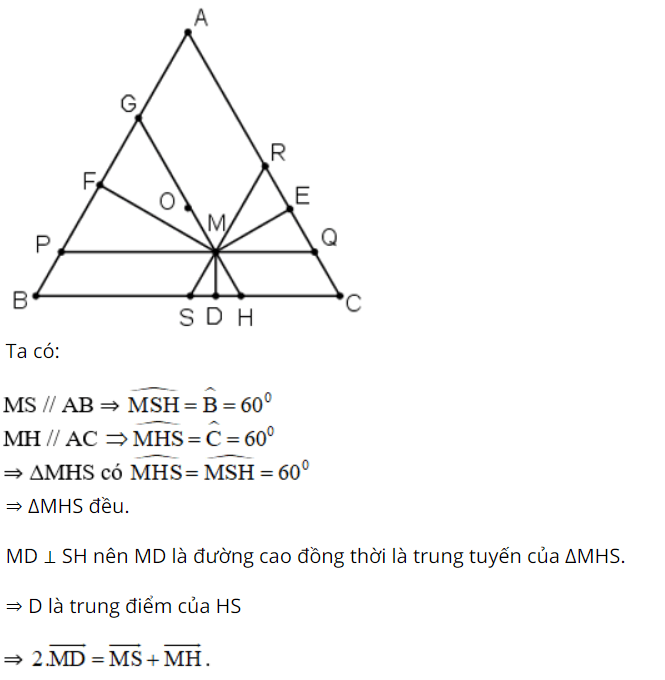
Bài 9 (trang 17 SGK Hình học 10):

Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.

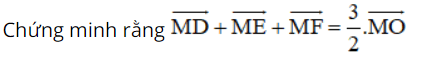
Trên đây là nội dung liên quan đến Tích Của Vectơ Với Một Số – Toán 10 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!