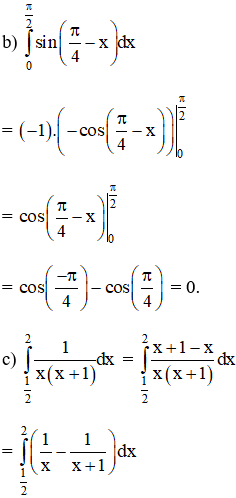Để học tốt Giải tích 12, phần này giúp bạn giải các bài tập trong sách giáo khoa Toán 12 được biên soạn bám sát theo nội dung sách Giải tích 12. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Tích Phân – Toán 12 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
Lý thuyết Tích phân
A. Tóm tắt lý thuyết
1. Định nghĩa
Cho f là hàm số liên tục trên đoạn [a; b] Giả sử F là một nguyên hàm của f trên [a; b] Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b] của hàm số f(x) kí hiệu là 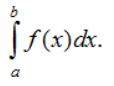
Ta dùng kí hiệu 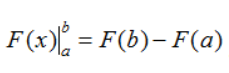 để chỉ hiệu số F(b) – F(a). Vậy
để chỉ hiệu số F(b) – F(a). Vậy 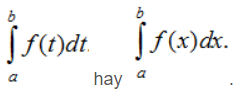 .
.
Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi 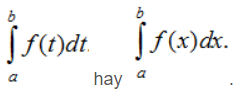 . Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
Ý nghĩa hình học của tích phân: Nếu hàm số f liên tục và không âm trên đoạn [a; b] thì tích phân 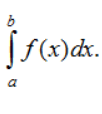 là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x) , trục Ox và hai đường thẳng x = a, x = b. Vậy S =
là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x) , trục Ox và hai đường thẳng x = a, x = b. Vậy S = 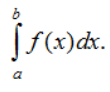
2. Tính chất của tích phân
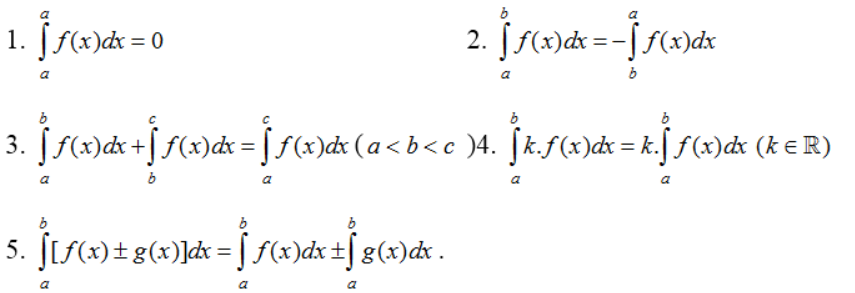
B. Kĩ năng giải bài tập
1. Một số phương pháp tính tích phân
I. Dạng 1: Tính tích phân theo công thức
Ví dụ 1: Tính các tính phân sau:
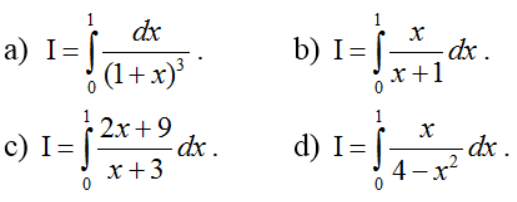
Hướng dẫn:
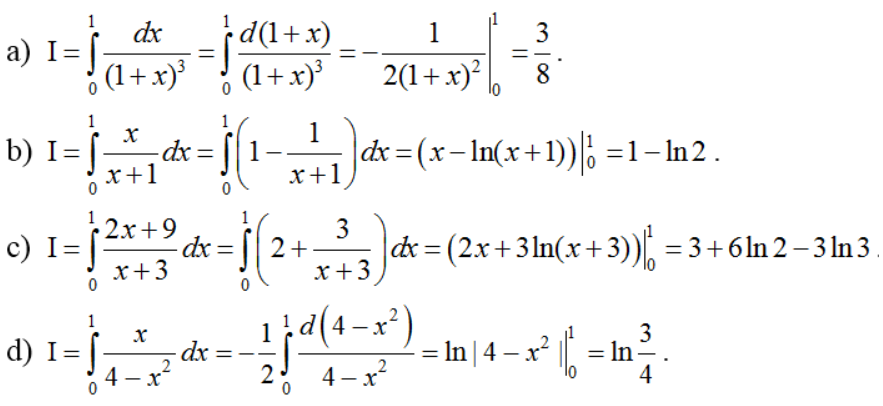
II. Dạng 2: Dùng tính chất cận trung gian để tính tích phân
Sử dụng tính chất 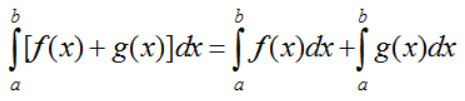 để bỏ dấu giá trị tuyệt đối.
để bỏ dấu giá trị tuyệt đối.
Ví dụ 2: Tính tích phân 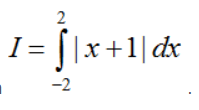 .
.
Hướng dẫn:
Nhận xét: 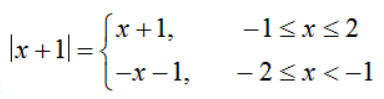 . Do đó
. Do đó
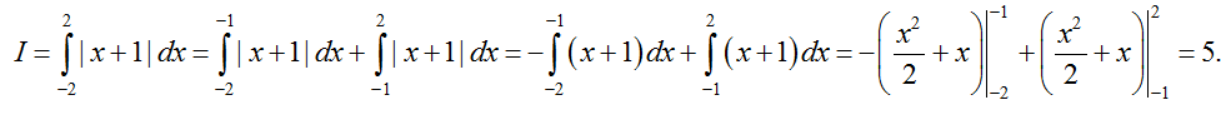
III. Dạng 3: Phương pháp đổi biến số
1) Đổi biến số dạng 1
Cho hàm số f liên tục trên đoạn [a; b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên đoạn [a; b] và α ≤ u(x) ≤ β. Giả sử có thể viết f(x) = g(u(x))u'(x), x ∈ [a; b] với g liên tục trên đoạn [α; β]. Khi đó, ta có
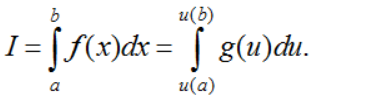
Ví dụ 3: Tính tích phân 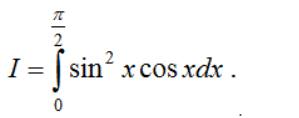 .
.
Hướng dẫn:
Đặt u = sinx. Ta có du = cosxdx. Đổi cận: x = 0 ⇒ u(0) = 0; x = π/2 ⇒ u(π/2) = 1
Khi đó 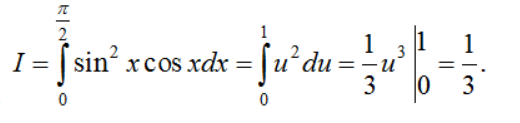
Dấu hiệu nhận biết và cách tính tính phân
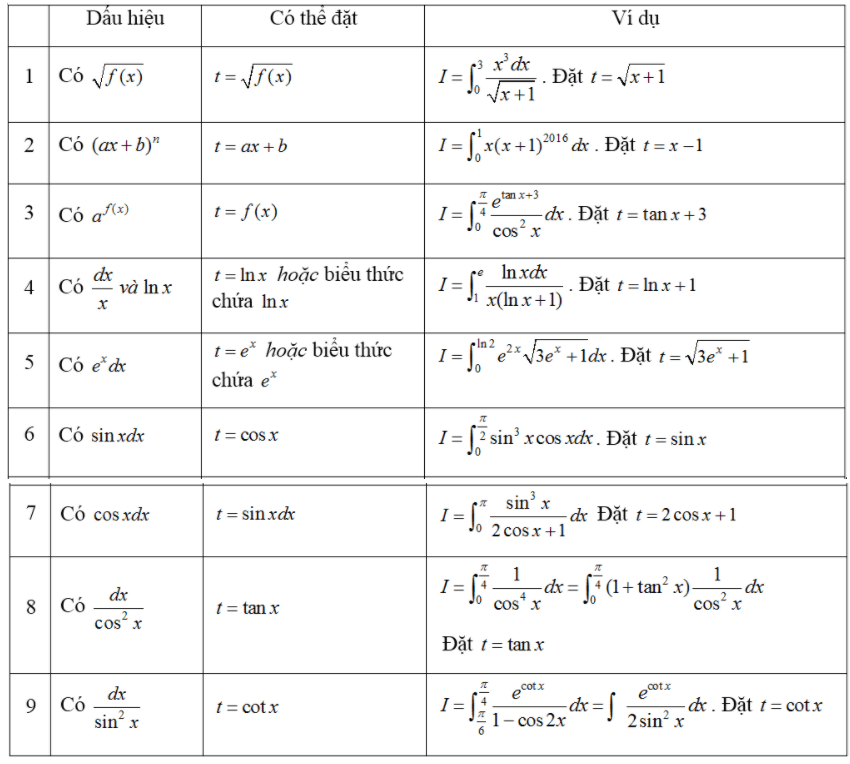 2) Đổi biến số dạng 2
2) Đổi biến số dạng 2
Cho hàm số f liên tục và có đạo hàm trên đoạn [a; b]. Giả sử hàm số x = φ(t) có đạo hàm và liên tục trên đoạn [α; β](*) sao cho φ(α) = a,φ(β) = b và a ≤ φ(t) ≤ b với mọi t ∈ [α; β]. Khi đó:
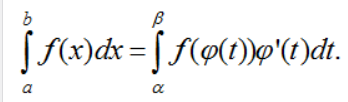
Một số phương pháp đổi biến: Nếu biểu thức dưới dấu tích phân có dạng
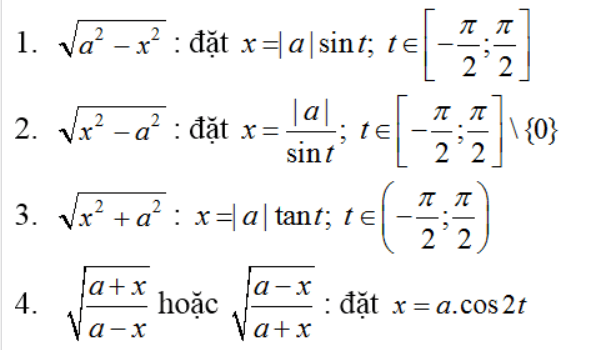
Lưu ý: Chỉ nên sử dụng phép đặt này khi các dấu hiệu 1, 2, 3 đi với x mũ chẵn. Ví dụ, để tính tích phân 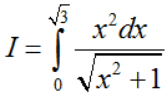 thì phải đổi biến dạng 2 còn với tích phân
thì phải đổi biến dạng 2 còn với tích phân 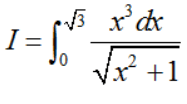 thì nên đổi biến dạng 1.
thì nên đổi biến dạng 1.
Ví dụ 4: Tính các tích phân sau:
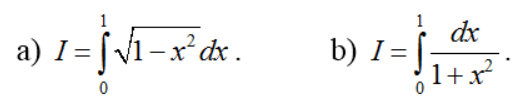
a) Đặt x = sint ta có dx = costdt. Đổi cận: x = 0 ⇒ t = 0; x = 1 ⇒ t = π/2.
Vậy 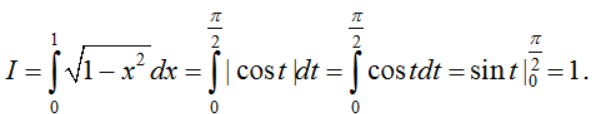
b) Đặt x = tant, ta có dx = (1 + tan2t)dt. Đổi cận: 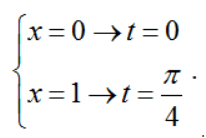 .
.
Vậy 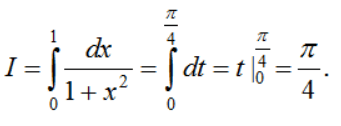
IV. Dạng 4: Phương pháp tính tích phân từng phần.
Định lí : Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm và liên tục trên đoạn [a; b] thì
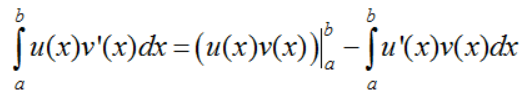
hay viết gọn là 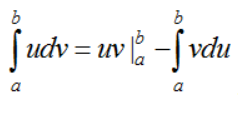 . Các dạng cơ bản: Giả sử cần tính
. Các dạng cơ bản: Giả sử cần tính 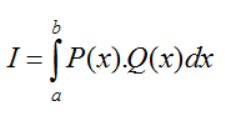
| Dạng hàm | P(x): Đa thức
Q(x): sin(kx) hay cos(kx) |
P(x): Đa thức
Q(x): ekx |
P(x): Đa thức
Q(x): ln(ax + b) |
P(x): Đa thức
Q(x): 1/sin2x hay 1/cos2x |
| Cách đặt | * u = P(x)
* dv là Phần còn lại của biểu thức dưới dấu tích phân |
* u = P(x)
* dv là Phần còn lại của biểu thức dưới dấu tích phân |
* u = ln(ax + b)
* dv = P(x)dx |
* u = P(x)
* dv là Phần còn lại của biểu thức dưới dấu tích phân |
Thông thường nên chú ý: “Nhất log, nhì đa, tam lượng, tứ mũ”.
Ví dụ 5: Tính các tích phân sau : 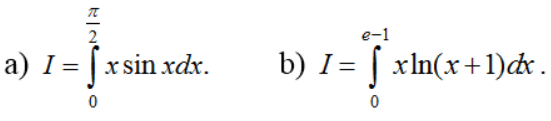
Hướng dẫn:
a) Đặt 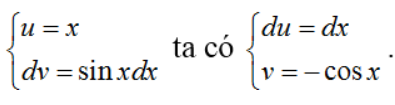
Do đó 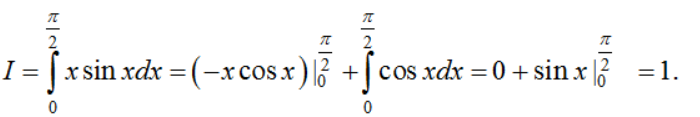
b) Đặt 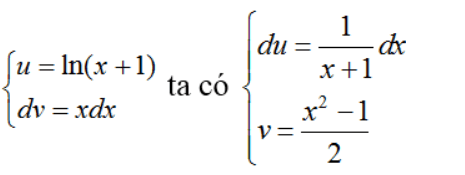
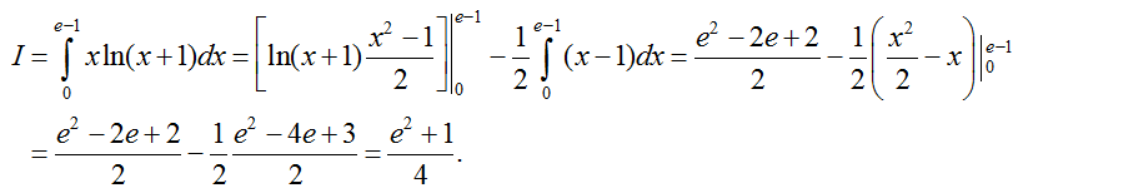
V. Giải bài Tập SGK
Bài 1 (trang 112 SGK Giải tích 12):
Tính các tích phân sau:
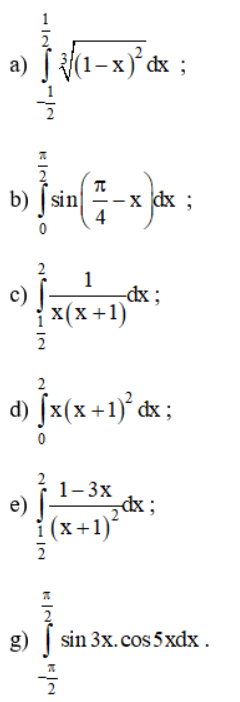
Lời giải:
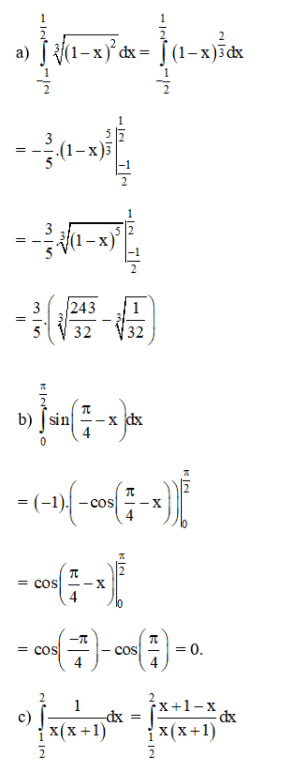
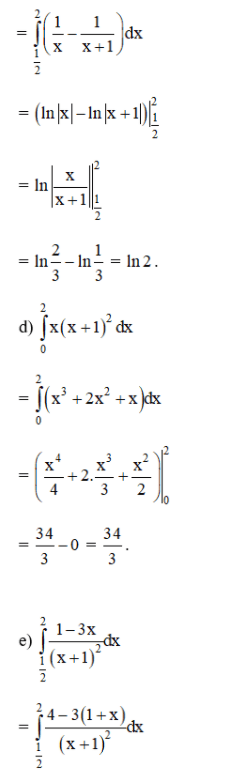
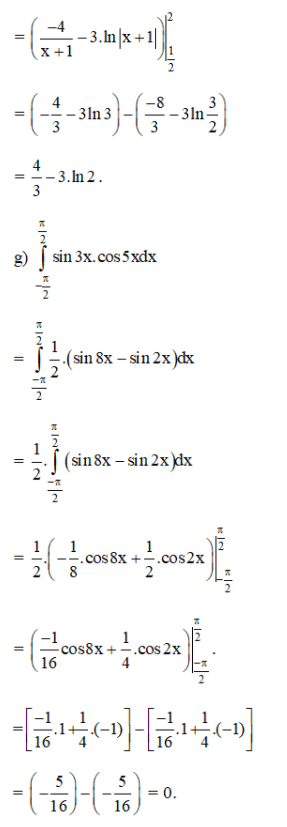
Bài 2 (trang 112 SGK Giải tích 12):
Tính các tích phân sau:
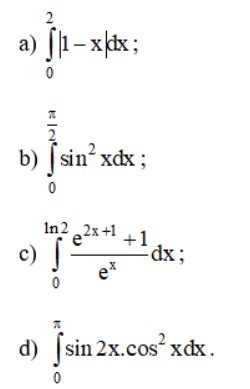
Lời giải:
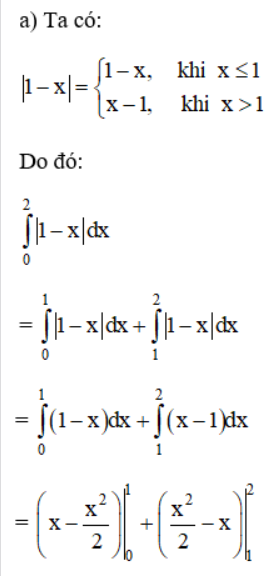
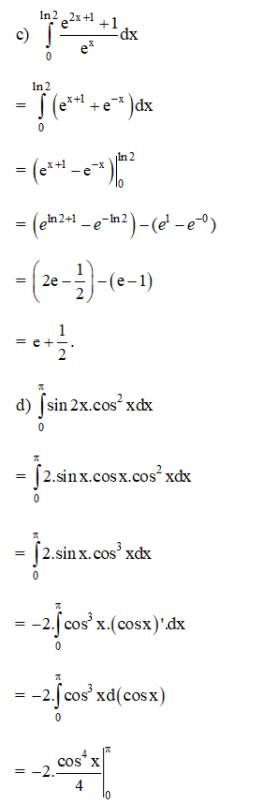
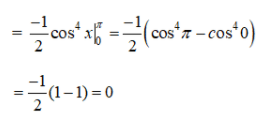
Bài 3 (trang 113 SGK Giải tích 12):
Sử dụng phương pháp đổi biến, hãy tính:
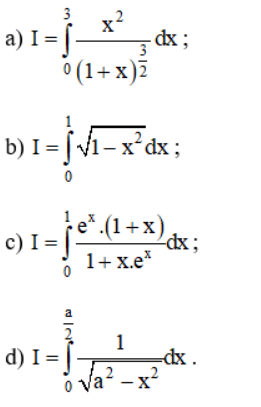
Lời giải:
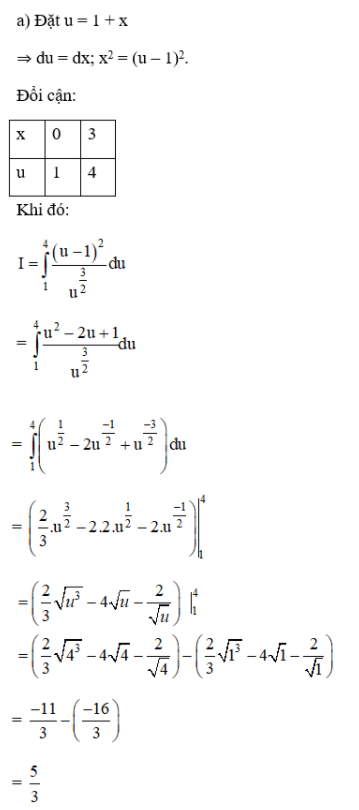
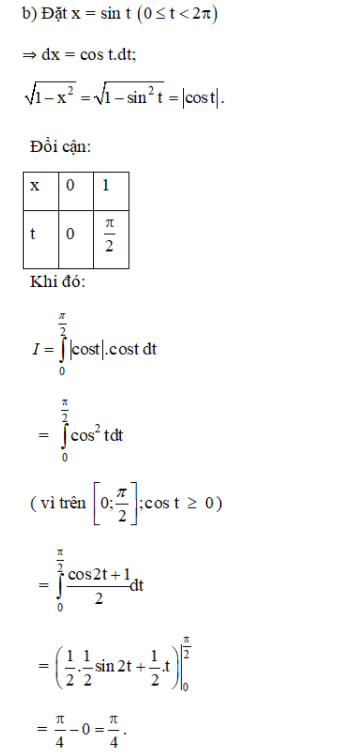
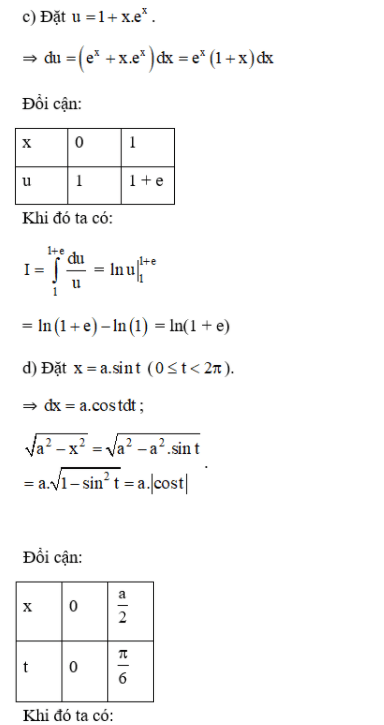
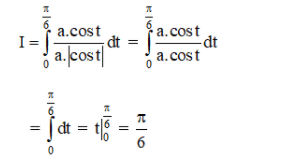
Bài 4 (trang 113 SGK Giải tích 12):
Sử dụng phương pháp tích phân từng phần, hãy tính:
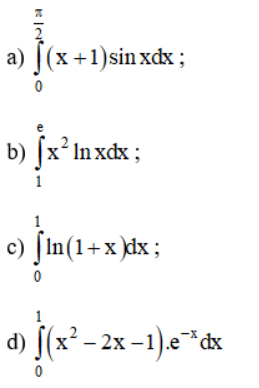
Lời giải:
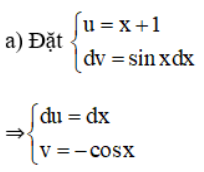
Theo công thức tích phân từng phần ta có:
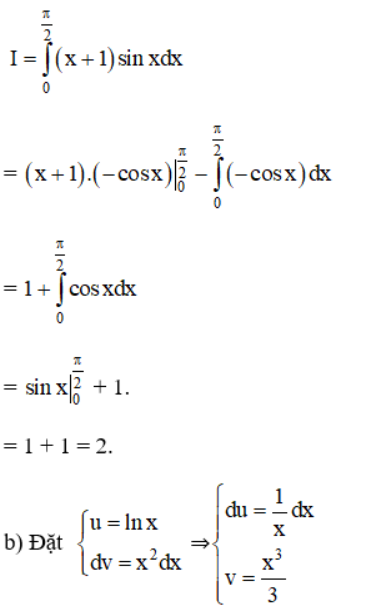
Theo công thức tích phân từng phần ta có:
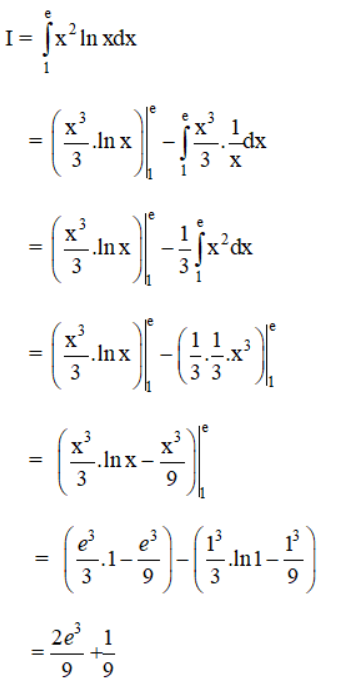

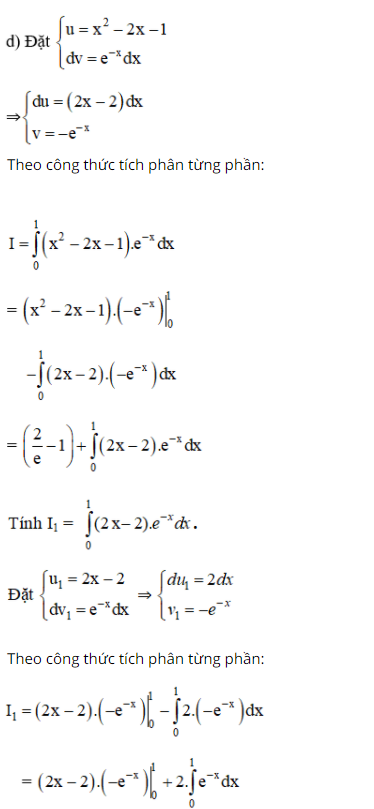
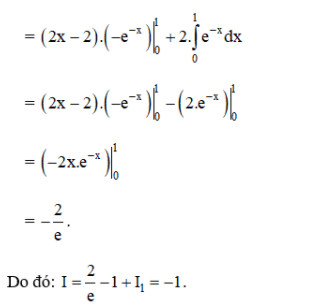
Bài 5 (trang 113 SGK Giải tích 12):
Tính các tích phân sau:
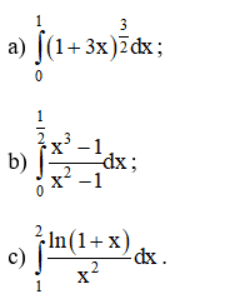
Lời giải:
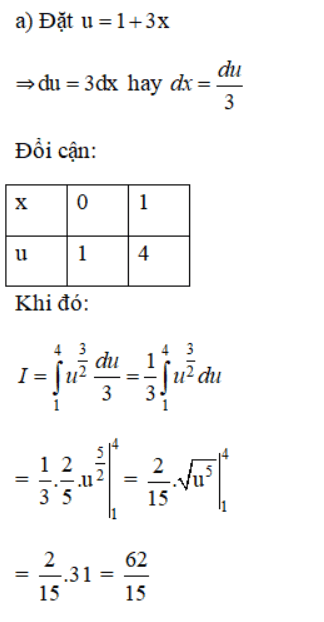
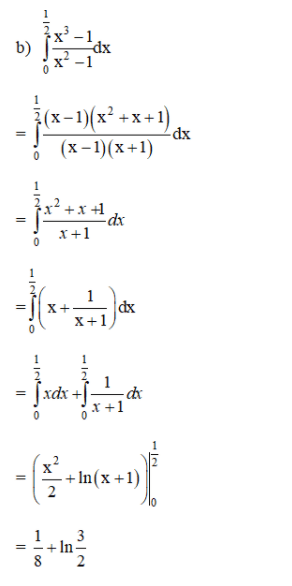
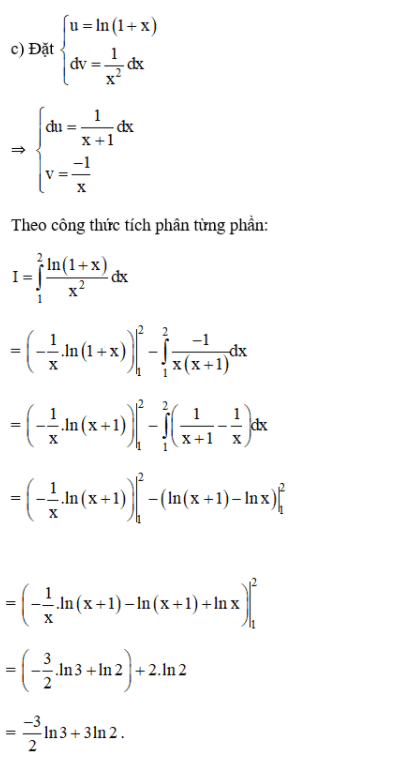
Bài 6 (trang 113 SGK Giải tích 12):
Tính 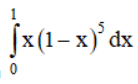 bằng hai phương pháp:
bằng hai phương pháp:
a) Đổi biến số u = 1 – x;
b) Tính tích phân từng phần.
Lời giải:
a) Đặt u = 1 – x;
⇒ du = -dx
Đổi biến :
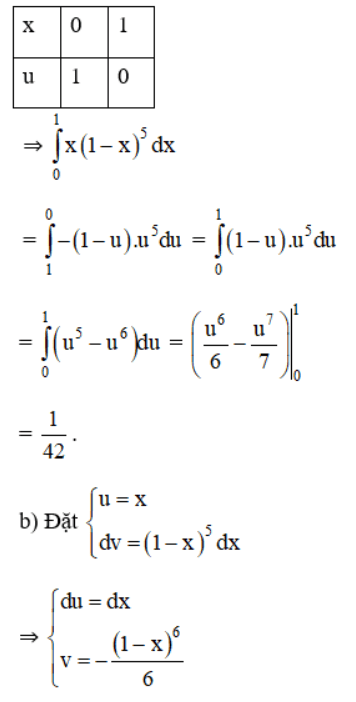
Theo công thức tích phân từng phần:
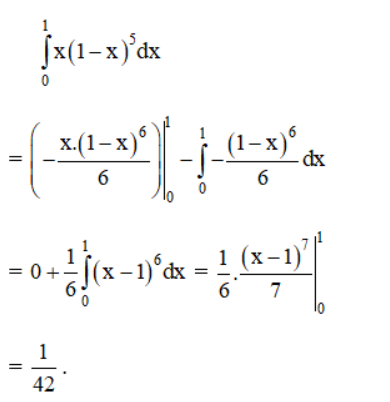
Trên đây là nội dung liên quan đến Tích Phân – Toán 12 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!