Để học tốt Giải tích 12, phần này giúp bạn giải các bài tập trong sách giáo khoa Toán 12 được biên soạn bám sát theo nội dung sách Giải tích 12. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Nguyên Hàm – Toán 12 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
I. Lý thuyết Nguyên hàm
A. Tóm tắt lý thuyết
I. NGUYÊN HÀM VÀ TÍNH CHẤT
1. Nguyên hàm
Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C
2. Tính chất của nguyên hàm
Tính chất 1: (∫f(x)dx)’ = f(x) và ∫f'(x)dx = f(x) + C
Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.
Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
4. Bảng nguyên hàm của một số hàm số sơ cấp
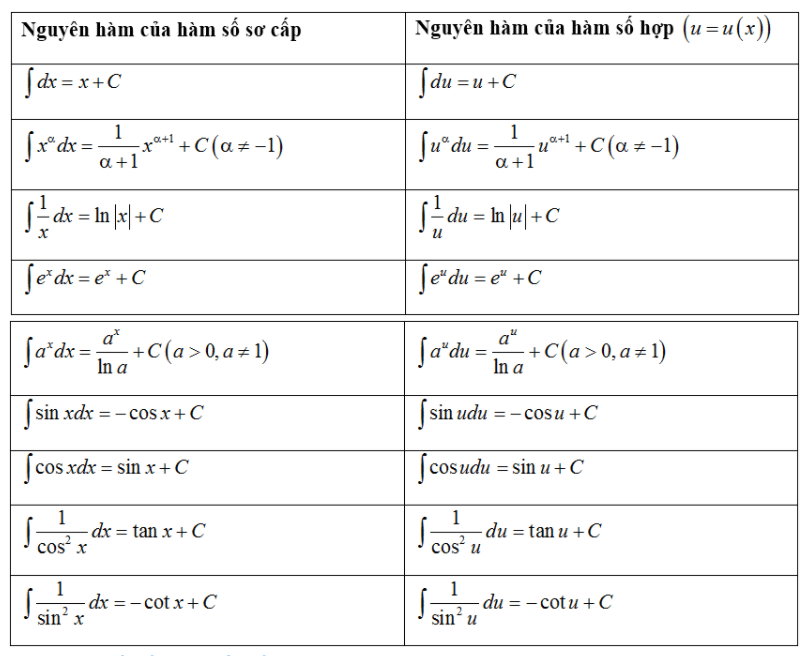
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
1. Phương pháp đổi biến số
Định lí 1: Nếu ∫f(u)du = F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì
∫f(u(x))u'(x)dx = F(u(x)) + C
Hệ quả: Nếu u = ax + b (a ≠ 0) thì ta có ∫f(ax + b)dx = (1/a)F(ax + b) + C
2. Phương pháp nguyên hàm từng phần
Định lí 2: Nếu hai hàm số u = u(x) và y = y(x) có đạo hàm liên tục trên K thì
∫u(x)v'(x)dx = u(x)v(x) – ∫u'(x)v(x)dx
Hay ∫udv = uv – ∫vdu
B. Kĩ năng giải bài tập
– Tìm nguyên hàm bằng phương pháp biến đổi trực tiếp.
– Tìm nguyên hàm bằng phương pháp đổi biến số.
– Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần.
III. Giải Bài Tập SGK
Bài 1 (trang 100 SGK Giải tích 12): Trong các cặp hàm số dưới đây, hàm số nào là nguyên hàm của hàm số còn lại?
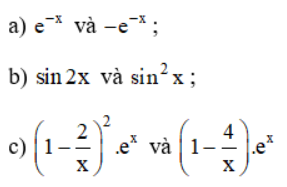
Lời giải:
a) Ta có: (-e-x)’ = -e-x.(-x)’ = e-x
⇒ -e-x là một nguyên hàm của hàm số e-x
Lại có : ( e-x )’ = e-x. (-x)’ = – e-x
Suy ra, e-x là một nguyên hàm của hàm số -e-x
Vậy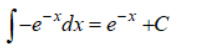 
b) (sin2x)’ = 2.sinx.(sinx)’ = 2.sinx.cosx = sin2x
⇒ sin2x là một nguyên hàm của hàm số .
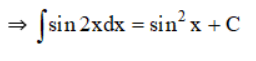
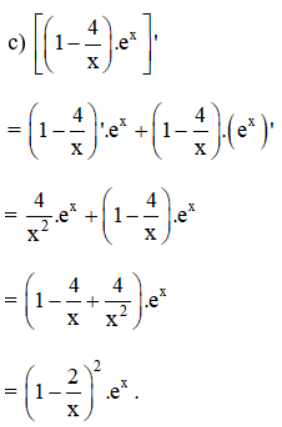
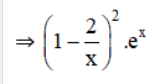là một nguyên hàm của hàm số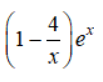 
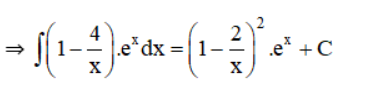
Bài 2 (trang 100 SGK Giải tích 12):
Tìm hiểu nguyên hàm của các hàm số sau:
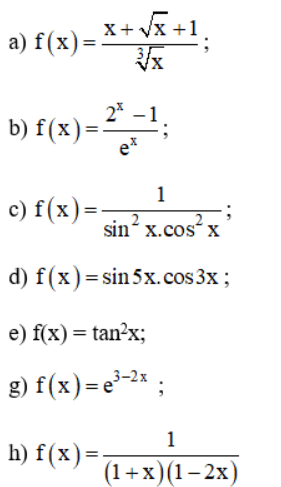
Lời giải:
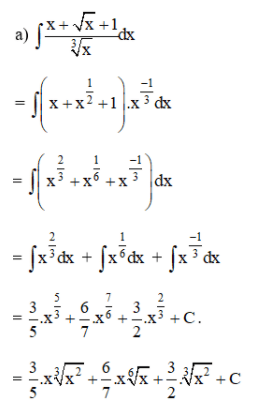
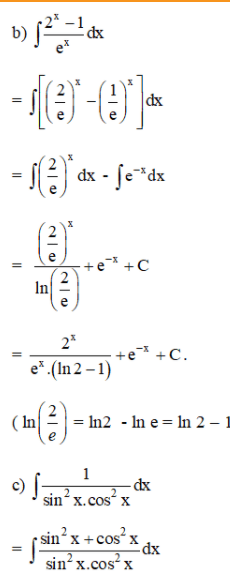
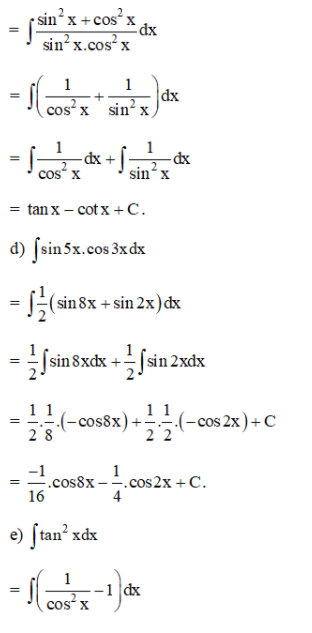
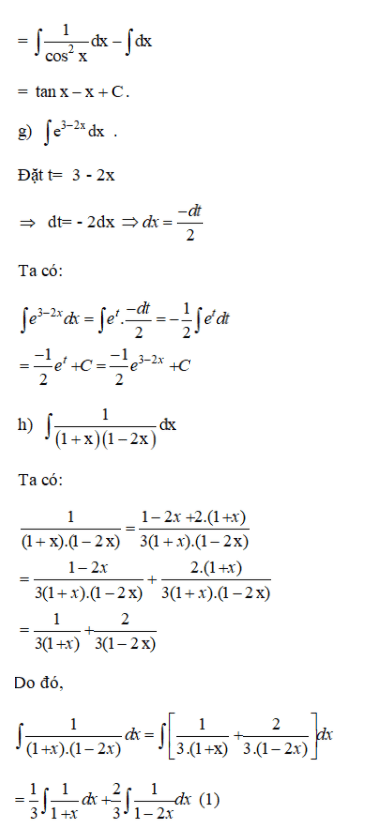
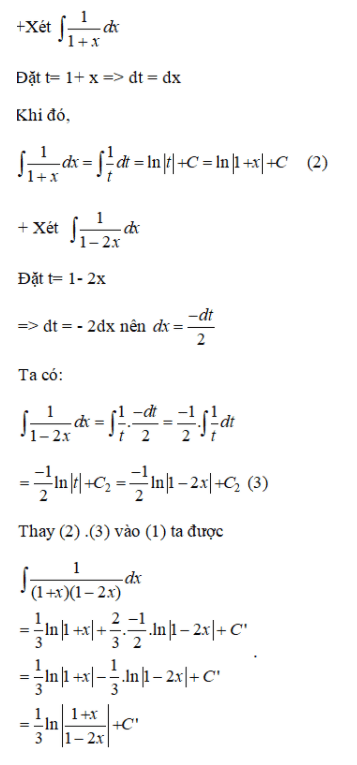
Bài 3 (trang 101 SGK Giải tích 12):
Sử dụng phương pháp đổi biến, hãy tính:
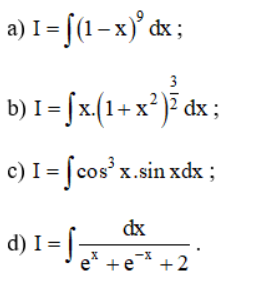
Lời giải:
a) Đặt u = 1 – x ⇒ u’(x) = -1⇒ du = -dx hay dx = – du
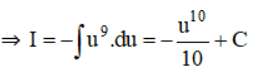
Thay u = 1 – x vào kết quả ta được :
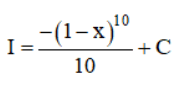
b) Đặt u = 1 + x2 ⇒ u’ = 2x ⇒ du = 2x.dx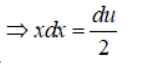 
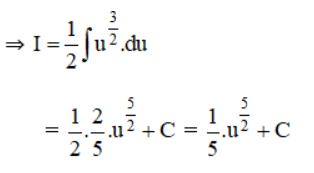
Thay lại u = 1+ x2 vào kết quả ta được:
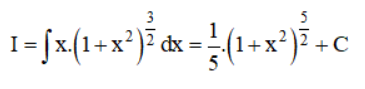
c) Đặt u = cosx ⇒ u’ = -sinx ⇒ du = -sinx.dx
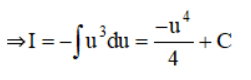
Thay lại u = cos x vào kết quả ta được:
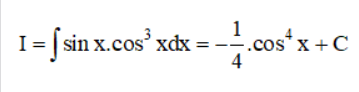
d) Ta có:
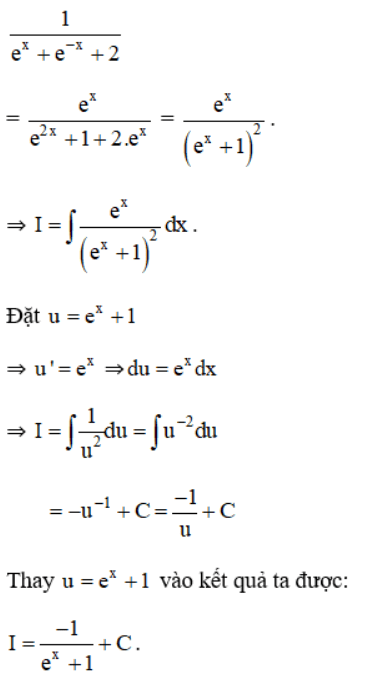
Bài 4 (trang 101 SGK Giải tích 12):
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính:
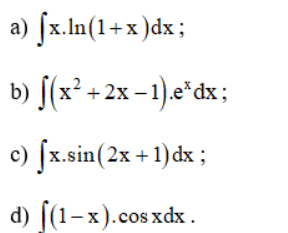
Lời giải:
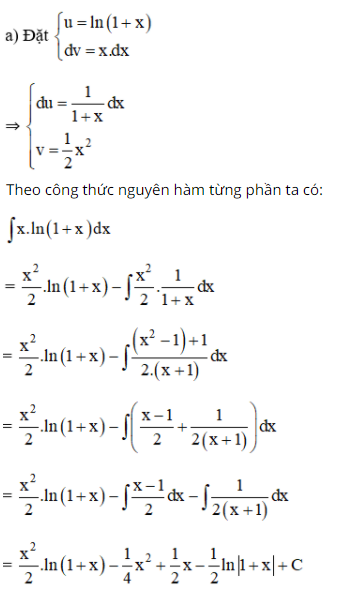
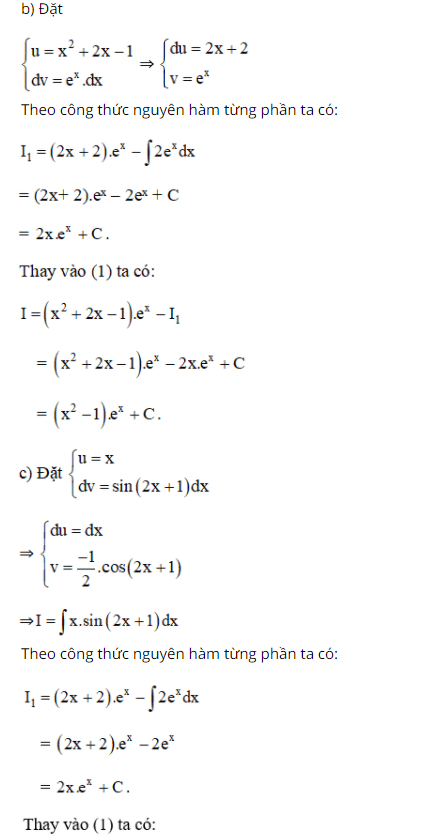
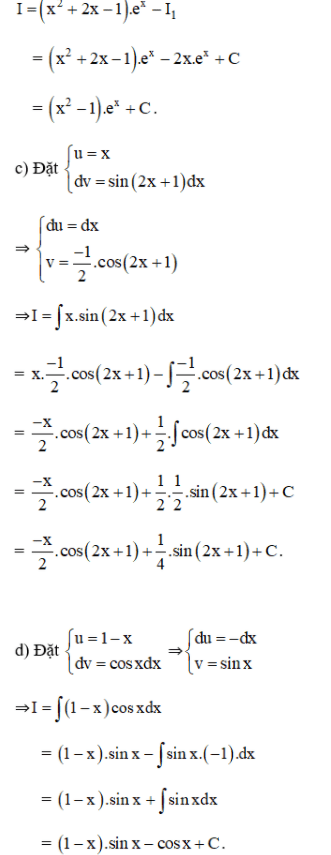
Trên đây là nội dung liên quan đến Nguyên Hàm – Toán 12 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!
