Để học tốt Hình Học 10, phần dưới giải các bài tập sách giáo khoa Toán 10 được biên soạn bám sát theo nội dung SGK Toán Hình Học 10. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Phương Trình Đường Thẳng – Toán 10 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!

I. Lý thuyết Phương trình đường thẳng

1. Vectơ chỉ phương của đường thẳng

Vectơ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu   và giá của song song hoặc trùng với ∆.

Nhận xét. Một đường thẳng có vô số vectơ chỉ phương.

2. Phương trình tham số của đường thẳng

Đường thẳng ∆ đi qua điểm M₀(x₀, y₀) và có VTCP  = (a; b)

=> phương trình tham số của đường thẳng ∆ có dạng

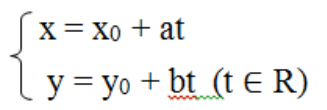
Nhận xét. Nếu đường thẳng ∆ có VTCP  = (a; b)

thì có hệ số góc k =

3. Vectơ pháp tuyến của đường thẳng

Vectơ  được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu   vuông góc với vectơ chỉ phương của ∆.

Nhận xét.

+) Một đường thẳng có vô số vectơ pháp tuyến.

4. Phương trình tổng quát của đường thẳng

Đường thẳng ∆ đi qua điểm M₀(x₀, y₀) và có VTPT  = (A; B)

=> phương trình tổng quát của đường thẳng ∆ có dạng

A(x – x₀) + B(y – y₀) = 0 hay Ax + By + C = 0 với C = –Ax₀ – By₀.

Nhận xét.

+) Nếu đường thẳng ∆ có VTPT = (A; B) thì có hệ số góc k =

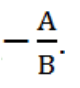
+) Nếu A, B, C đều khác 0 thì ta có thể đưa phương trình tổng quát về dạng

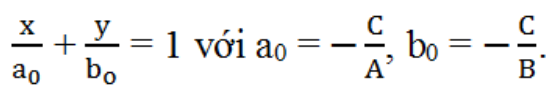
Phương trình này được gọi là phương trình đường thẳng theo đoạn chắn, đường thẳng này cắt Ox và Oy lần lượt tại M(a0; 0) và N(0; b0).

5. Vị trí tương đối của hai đường thẳng

Xét hai đường thẳng có phương trình tổng quát là

∆₁: a₁x + b₁y + c₁ = 0 và ∆₂: a₂x + b₂y + c₂ = 0

Tọa độ giao điểm của ∆₁ và ∆₂ là nghiệm của hệ phương trình:

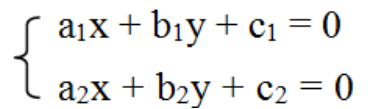
+) Nếu hệ có một nghiệm (x₀; y₀) thì ∆₁ cắt ∆₂ tại điểm M₀(x₀, y₀).

+) Nếu hệ có vô số nghiệm thì ∆₁ trùng với ∆₂.

+) Nếu hệ vô nghiệm thì ∆₁ và ∆₂ không có điểm chung, hay ∆₁ song song với ∆₂

Cách 2. Xét tỉ số

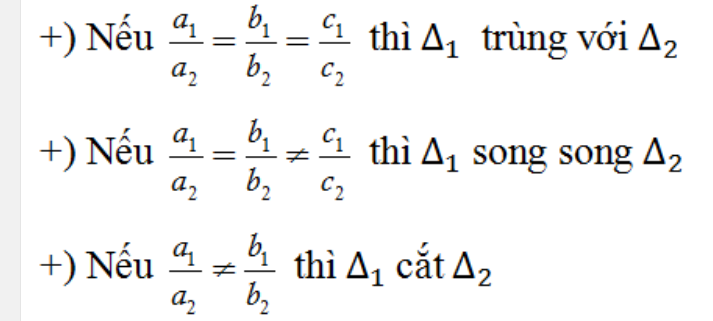
6. Góc giữa hai đường thẳng

Cho hai đường thẳng

∆₁: a₁x + b₁y + c₁ = 0 có VTPT  = (a₁; b₁);

∆₂: a₂x + b₂y + c₂ = 0 có VTPT  = (a₂; b₂);

Gọi α là góc tạo bởi giữa hai đường thẳng ∆₁ và ∆₂

Khi đó

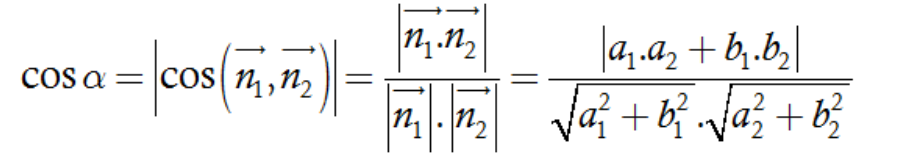
7. Khoảng cách từ một điểm đến một đường thẳng

Khoảng cách từ M₀(x₀, y₀) đến đường thẳng ∆: ax + by + c = 0 được tính theo công thức

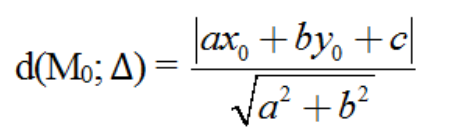
Nhận xét. Cho hai đường thẳng ∆₁: a₁x + b₁y + c₁ = 0 và ∆₂: a₂x + b₂y + c₂ = 0 cắt nhau thì phương trình hai đường phân giác của góc tạo bởi hai đường thẳng trên là:

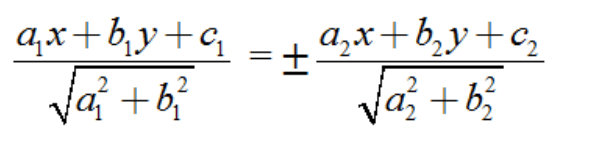
II. Phương trình đường tròn

1. Phương trình đường tròn có tâm và bán kính cho trước

Trong mặt phẳng Oxy, đường tròn (C ) tâm I(a; b) bán kính R có phương trình:

(x – a)² + (y – b)² = R²

Chú ý. Phương trình đường tròn có tâm là gốc tọa độ O và bán kính R là x² + y² = R²

2. Nhận xét

+) Phương trình đường tròn (x – a)² + (y – b)² = R² có thể viết dưới dạng

x² + y² – 2ax – 2by + c = 0

trong đó c = a² + b² – R².

+) Phương trình x² + y² – 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi a² + b² – c² > 0. Khi đó, đường tròn (C) có tâm I(a; b), bán kính R =

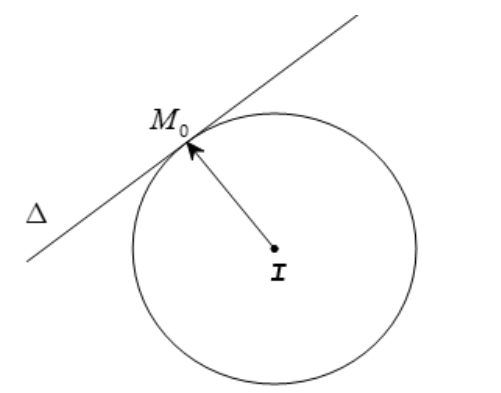
3. Phương trình tiếp tuyến của đường tròn

Cho đường tròn (C) có tâm I(a; b) và bán kính R.

Đường thẳng Δ là tiếp tuyến với (C) tại điểm M_o(x_o; y_o).

Ta có

+) M_o(x_o; y_o) thuộc Δ.

+) = (x0 – a; y0 – b) là vectơ pháp tuyến của Δ.

Do đó Δ có phương trình là

(x_o – a).(x – x_o) + (y_o – b).(y – y_o) = 0.

Phương trình đường elip

1. Định nghĩa: Cho hai điểm cố định F₁ và F₂ với F₁F₂ = 2c (c > 0). Tập hợp các điểm M thỏa mãn MF1 + MF2 = 2a (a không đổi và a > c > 0) là một đường Elip.

+) F₁, F₂ là hai tiêu điểm.

+) F₁F₂ = 2c là tiêu cự của Elip

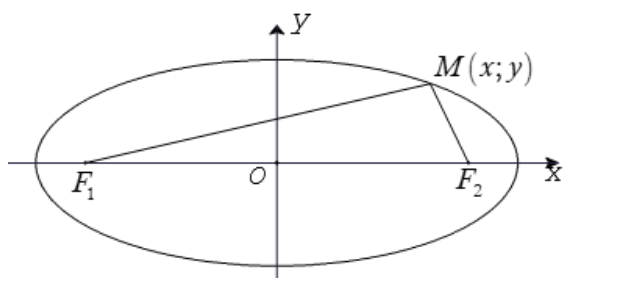
2. Phương trình chính tắc của Elip

(E): 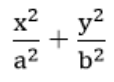 = 1 với a² = b² + c²

Do đó điểm M(x_o; y_o) ∈ (E) <=> 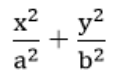 = 1 và |x_o| ≤ a, |y_o| ≤ b.

3. Tính chất và hình dạng của Elip

+) Trục đối xứng Ox (chứa trục lớn), Oy (chứa trục bé).

+) Tâm đối xứng O.

+) Tọa độ các đỉnh A₁(–a; 0), A₂(a; 0), B₁(0; –b), B₂(0; b).

+) Độ dài trục lớn 2a. Độ dài trục bé 2b.

+) Tiêu điểm F₁(–c; 0), F₂(c; 0).

+) Tiêu cự 2c.

II. Giải Bài Tập SGK

Bài 1 (trang 80 SGK Hình học 10):

Lập phương trình tham số của đường thằng d trong mỗi trường hợp sau:

a) d đi qua điểm M(2; 1) và có vec tơ chỉ phương  ;

b) d đi qua điểm M(–2; 3) và có vec tơ pháp tuyến  .

Lời giải

a) Phương trình tham số của d là:

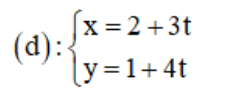
b) d nhận  là 1 vec tơ pháp tuyến

⇒ d nhận  là 1 vec tơ chỉ phương

Phương trình tham số của đường thẳng d là:

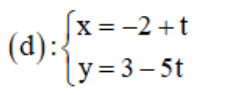
Bài 2 (trang 80 SGK Hình học 10):

Lập phương trình tổng quát của đường thẳng Δ trong mỗi trường hợp sau:

a) Δ đi qua M(–5; –8) và có hệ số góc k = –3;

b) Δ đi qua hai điểm A(2; 1) và B(–4; 5).

Lời giải

a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:

y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.

b) Ta có: A(2; 1), B(–4; 5) ⇒

Δ đi qua hai điểm A(2; 1) và B(–4; 5)

⇒ Δ nhận  là một vtcp

⇒ Δ nhận  là một vtpt.

Phương trình tổng quát của đường thẳng Δ là:

(Δ) : 4(x – 2) + 6(y -1) = 0

Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.

Bài 3 (trang 80 SGK Hình học 10):

Cho tam giác ABC biết A(1; 4), B(3; -1) và C(6; 2).

a, Lập phương trình tổng quát của các đường thẳng AB, BC và CA.

Lời giải

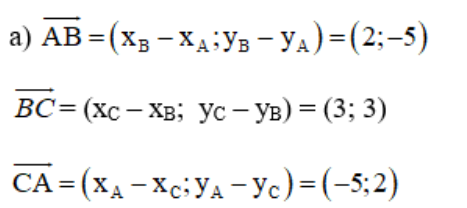
+ Lập phương trình đường thẳng AB:

Đường thẳng AB nhận là 1 vtcp ⇒ AB nhận  là 1 vtpt

Mà A(1; 4) thuộc AB

⇒ PT đường thẳng AB: 5(x- 1) + 2(y – 4) = 0 hay 5x + 2y – 13 = 0.

+ Lập phương trình đường thẳng BC:

Đường thẳng BC nhận là 1 vtcp ⇒ BC nhận  là 1 vtpt

Mà B(3; –1) thuộc BC

⇒ Phương trình đường thẳng BC: 1(x – 3) – 1(y + 1) = 0 hay x – y – 4 = 0.

+ Lập phương trình đường thẳng CA:

Đường thẳng CA nhận là 1 vtcp ⇒ CA nhận  là 1 vtpt

Mà C(6; 2) thuộc CA

⇒ Phương trình đường thẳng AC: 2(x – 6) + 5(y – 2) = 0 hay 2x + 5y – 22 = 0.

b) + AH là đường cao của tam giác ABC ⇒ AH ⊥ BC

⇒ Đường thẳng AH nhận 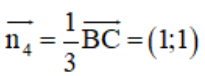 là 1 vec tơ pháp tuyến

Mà A(1; 4) thuộc AH

⇒ Phương trình đường thẳng AH: 1(x – 1) + 1(y – 4) = 0 hay x + y – 5 = 0.

+ Trung điểm M của BC có tọa độ 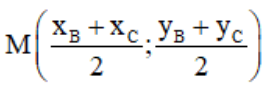hay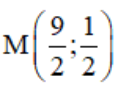

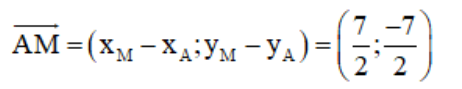
Đường thẳng AM nhận  là 1 vtcp

⇒ AM nhận 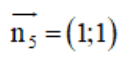 là 1 vtpt

Mà A(1; 4) thuộc AM

⇒ Phương trình đường thẳng AM: 1(x – 1) + 1(y – 4) = 0 hay x + y – 5 = 0.

Bài 4 (trang 80 SGK Hình học 10):

Viết phương trình tổng quát của đường thẳng đi qua điểm M(4; 0) và điểm N(0; -1).

Lời giải

Đường thẳng MN nhận  là 1 vtcp

⇒ MN nhận  là 1 vtpt

Mà M(4; 0) thuộc đường thẳng MN

⇒ Phương trình đường thẳng MN: 1(x – 4) – 4(y – 0) = 0 hay x – 4y – 4 = 0.

Bài 5 (trang 80 SGK Hình học 10):

Xét vị trí tương đối của các cặp đường thẳng d₁ và d₂ sau đây:

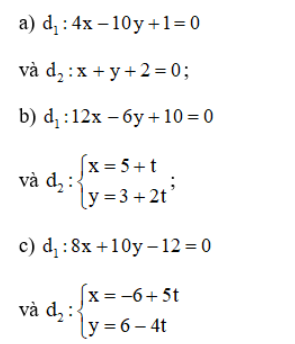
Lời giải

Cách 1: Dựa vào số nghiệm của hệ phương trình:

a) Xét hệ phương trình

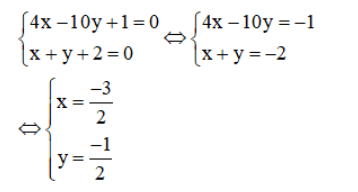
Hệ phương trình có nghiệm duy nhất nên (d₁) cắt (d₂).

b) Xét hệ phương trình

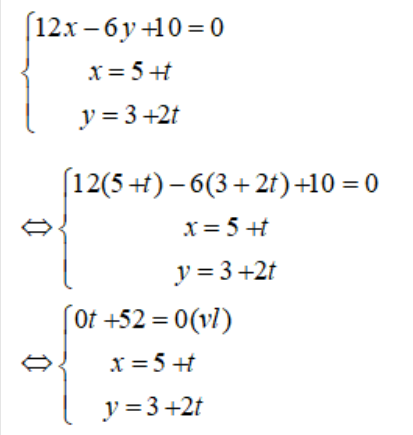
Hệ phương trình trên vô nghiệm nên hai đường thẳng trên song song.

c) Xét hệ phương trình

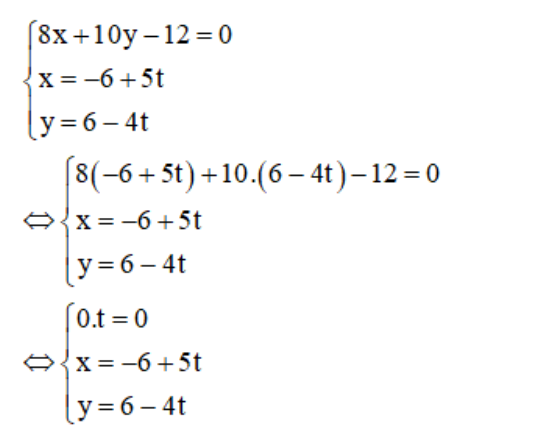
Hệ phương trình trên có vô số nghiệm nên hai đường thẳng trùng nhau.

Cách 2: Dựa vào vị trí tương đối của các vectơ chỉ phương (hoặc vectơ pháp tuyến).

a) d₁ nhận  là một vectơ pháp tuyến

d₂ nhận  là 1 vtpt

Nhận thấy  không cùng phương nên d₁ cắt d₂.

b) d₁ nhận  là 1 vtpt ⇒ d₁ nhận  là 1 vtcp

d₂ nhận 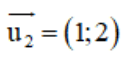 là 1 vtcp.

Nhận thấy  cùng phương

⇒ d₁ và d₂ song song hoặc trùng nhau.

Xét điểm M(5;3) có:

M(5; 3) ∈ d₂

12.5 – 6.3 + 10 = 52 ≠ 0 nên M(5; 3) ∉ d₁.

Vậy d₁ và d₂ song song.

c) d₁ nhận  là 1 vtpt ⇒ d₁ nhận  là 1 vtcp.

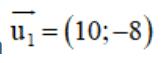d₂ nhận  là 1 vtcp.

Nhận thấy  cùng phương

⇒ d₁ và d₂ song song hoặc trùng nhau.

Xét M(–6; 6) ∈ d₂; M(–6; 6) ∈ d₁ (Vì 8.(–6) + 10.6 – 12 = 0)

⇒ d₁ và d₂ trùng nhau.

Bài 7 (trang 81 SGK Hình học 10):

Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d₁: 4x – 2y + 6 = 0 và d₂: x – 3y + 1 = 0

Lời giải

Với d₁: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n₁→(4;-2)

và d₂: x – 3y + 1 = 0 có vecto pháp tuyến là: n₂→(1;-3) ; ta có :

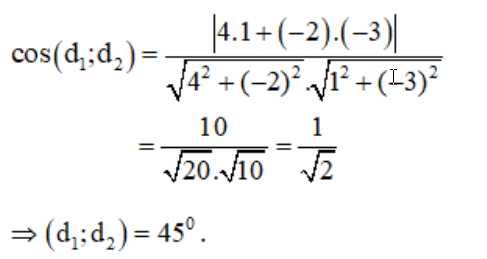
Trên đây là nội dung liên quan đến Phương Trình Đường Thẳng – Toán 10 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!