Công thức tính nguyên hàm từ cơ bản đến nâng cao và bảng nguyên hàm đầy đủ là một phần kiến thức không thể thiếu trong trương trình giải tích lớp 12 và cũng xuất hiện khá nhiều trong các đề thi đại học, THPT. Dưới đây là bảng nguyên hàm của tất các hàm số phố biến thường gặp nhất chi tiết nhất, mời các bạn cùng tham khảo!
1. Nguyên hàm là gì ? Khái niệm về nguyên hàm và tính chất
1.1. Khái niệm về nguyên hàm
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng của R.
Định nghĩa:
Cho hàm số f(x) xác định trên K.
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F′(x)=f(x)với mọi x∈K
Ngoài ra một số định nghĩa tương đương của các tài liệu khác cho các bạn tham khảo:

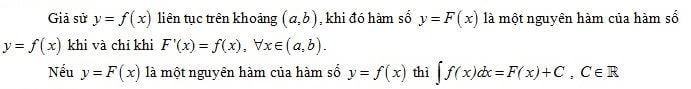
Định lý 1:
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x)=F(x)+C cũng là một nguyên hàm của hàm số f(x) trên K.
Định lý 2:
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x)+C với C là một hằng số tùy ý.
Kí hiệu họ nguyên hàm của hàm số f(x) là ∫f(x)dx.
Khi đó : ∫f(x)dx=F(x)+C,C∈R.
Định lí 3:
Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
1.2. Tính chất nguyên hàm
Tính chất 1: ∫f′(x)dx=f(x)+C,C∈R.
Tính chất 2: ∫fk(x)dx=k∫f(x)dx (với k là hằng số khác 0).
Tính chất 3: ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx.
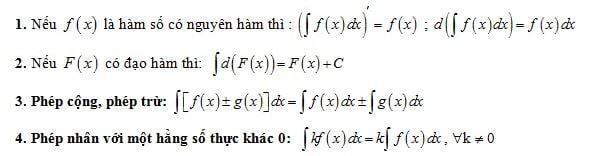
2. Một số bảng nguyên hàm cơ bản thường gặp

3. Công thức tính nguyên hàm từ cơ bản đến nâng cao, đầy đủ và chi tiết nhất
3.1. Công thức tính nguyên hàm cơ bản thường gặp ( Vô tỉ, hữu Tỉ, hàm mũ, hàm E, hàm lượng giác)
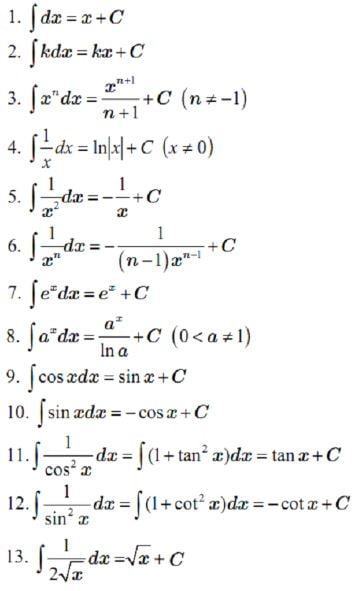
3.2. Công thức tính nguyên hàm cơ bản thường gặp ( Vô tỉ, hữu Tỉ, hàm mũ, hàm E, hàm lượng giác)
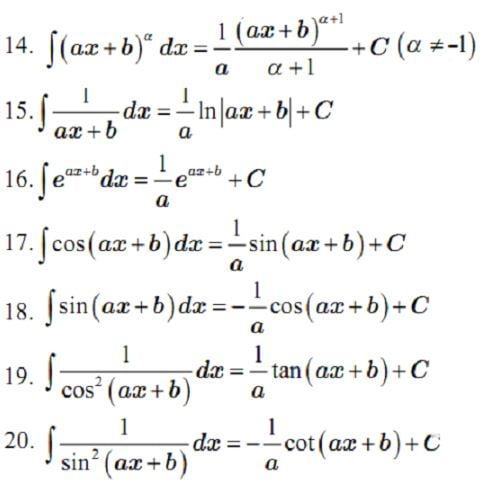
3.3. Công thức tính nguyên hàm cơ bản thường gặp ( Vô tỉ, hữu Tỉ, hàm mũ, hàm E, hàm lượng giác)

4. Video công thức tính nguyên hàm
Bên trên là bảng nguyên hàm, công thức tính nguyên hàm đầy đủ và chi tiết nhất. Mọi thắc mắc về bảng nguyên hàm, công thức tính nguyên hàm từ cơ bản đến năng cao dean2020 mong sẽ giúp được chút kiến thức cho các bạn. Việc ghi nhớ và thành thạo bảng nguyên hàm là điều bắt buộc đối với các em. Các em hãy liệt kê các công thức thường dùng để có thể dễ dàng xem lại khi cần. Điều này sẽ rất hiệu quả nếu các em bắt đầu học một phần mới. Việc phân biệt nguyên hàm và vi phân cũng cần phải nhớ, và cũng đừng nhầm lẫn giữa nguyên hàm lượng giác.




