Để học tốt Giải tích 12, phần này giúp bạn giải các bài tập trong sách giáo khoa Toán 12 được biên soạn bám sát theo nội dung sách Giải tích 12. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Cộng Trừ Và Nhân Số Phức – Toán 12 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
Lý thuyết Cộng, trừ và nhân số phức
A. Tóm tắt lý thuyết
Cho hai số phức z1 = a + bi và z2 = c + di thì:
• Phép cộng số phức: z1 + z2 = (a + c) + (b + d)i
• Phép trừ số phức: z1 – z2 = (a – c) + (b – d)i
– Mọi số phức z = a + bi thì số đối của z là -z = -a – bi: z + (-z) = (-z) + z = 0
• Phép nhân số phức: z1.z2 = (ac – bd) + (ad + bc)i
• Phép chia số phức: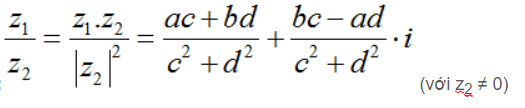
– Chú ý :
• Với mọi số thực k và mọi số phức z = a + bi thì:
k(a + b)i = ka + kbi
• Với mọi số phức: 0z = 0
• Phép cộng và phép nhân các số phức có tất cả các tính chất của phép cộng và phép nhân của số thực.
• i4k = 1; i4k + 1 = i; i4k + 2 = -1; i4k + 3 = -i
Ví dụ 1: Cho số phức z = 2 + 5i . Tìm số phức w = iz + z−.
A. w = 7 – 3i. B. w = -3 – 3i. C. w = 3 = 3i. D. w = -7 – 7i.
Hướng dẫn:
Ta có: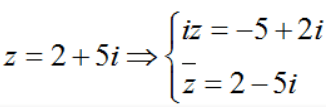 
⇔ w = iz + z− = (-5 + 2) + (2 – 5)i = -3 – 3i.
Vậy chọn đáp án B.
Ví dụ 2: Cho số phức z = (1 – 6i) – (2 – 4i). Phần thực, phần ảo của z lần lượt là
A. -1; -2. B. 1; 2. C. 2;1. D. – 2;1.
Hướng dẫn:
Ta có : z = (1 – 6i) – (2 – 4i) = -1 -2i
Vậy chọn đáp án A.
Ví dụ 3: Cho số phức z = (2 + i)(1 – i) + 1 + 3i. Tính môđun của z.
A. 4√2. B. √13. C. 2√2. D. 2√5.
Hướng dẫn:
Ta có: z = (2 + i)(1 – i) + 1 + 3i = (2.1 + 1.1) + (-1.2 + 1.1)i + 1 + 3i = 4 + 2i
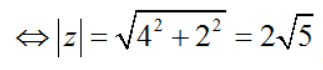. Vậy chọn đáp án D.
II. Giải Bài Tập SGK
Bài 1 (trang 135 SGK Giải tích 12):
Thực hiện các phép tính sau:
a) (3 – 5i) + (2 + 4i)
b) (-2 – 3i) + (-1 – 7i)
c) (4 + 3i) – (5 – 7i)
d) (2 – 3i) – (5 – 4i)
Lời giải:
a) Ta có: (3 – 5i) + (2 + 4i) = (3 + 2) + (-5 + 4)i = 5 – i
b) Ta có: (-2 – 3i) + (-1 – 7i) = (-2 – 1) + (-3 – 7)i = -3 – 10i
c) Ta có: (4 + 3i) – (5 – 7i) = (4 – 5) + [3 – (-7)]i = -1 + 10i
d) Ta có: (2 – 3i) – (5 – 4i) = (2 – 5) + (-3 + 4)i = -3 + i
Bài 2 (trang 136 SGK Giải tích 12):
Tính α+ β,α- β với:
a) α = 3, β = 2i
b) α = 1 – 2i, β = 6i
c) α = 5i, β = -7i
d) α = 15; β = 4 – 2i
Lời giải:
a) Ta có: α + β = 3 + 2i ; α – β = 3 – 2i
b) α + β = (1 – 2i) + 6i = 1 + 4i;
α – β = (1 – 2i) – 6i = 1 – 8i
c) α + β = 5i + (-7i) = -2i;
α – β = 5i – (-7i) = 12i
d) α + β = 15 + (4 – 2i) = 19 – 2i ;
α – β = 15 – (4 – 2i) = 11 + 2i
Bài 3 (trang 136 SGK Giải tích 12):
Thực hiện các phép tính sau:
a) (3 – 2i)(2 – 3i)
b) (-1 + i)(3 + 7i)
c) 5(4 + 3i)
d) (-2 – 5i)4i
Lời giải:
a) (3 – 2i)(2 – 3i) = 3. 2 – 3. 3i – 2i.2 – 2i. (- 3i) = 6 – 9i – 4i – 6 = ( 6- 6) + ( -9 – 4).i = -13i
b) (-1 + i)(3 + 7i) = -1.3 + (-1).7i +i.3 + i. 7i = -3 – 7i + 3i – 7 =( -3 – 7)+ ( – 7+3) i = -10 – 4i
c) 5(4 + 3i) = 5.4 + 5.3i = 20 + 15i
d) (-2 – 5i).4i = – 2. 4i – 5i. 4i = – 8i + 20 = 20 – 8i
Bài 4 (trang 136 SGK Giải tích 12):
Tính i3,i4;i5. Nêu cách tính in với n là số tự nhiên tùy ý:
Lời giải:
+ i3 = i2.i= – 1i = -i.
i4 = i2.i2 = -1.(-1) = 1
i5 = i4.i = 1.i = i
+ Với n là số tự nhiên bất kì ta có :
Nếu n = 4k ⇒ in = i4k = (i4)k = 1k = 1.
Nếu n = 4k + 1 ⇒ in = i4k + 1 = i4k.i = 1.i = i.
Nếu n = 4k + 2 ⇒ in = i4k + 2 = i4k.i2 = 1.(-1) = -1.
Nếu n = 4k + 3 ⇒ in = i4k + 3 = i4k.i3 = 1.(-i) = -i.
Bài 5 (trang 136 SGK Giải tích 12):
Tính:
a) (2 + 3i)2
b) (2 + 3i)3
Lời giải:
a) Ta có: (2 + 3i)2 = 22 + 2.2.3i + (3i)2 = 4 + 12i – 9 = ( 4- 9) + 12i = – 5 + 12i
Tổng quát (a + bi)2 = a2 – b2 + 2abi
b) Ta có:
(2 + 3i)3 = (2 + 3i)2.(2 + 3i)
= (-5 + 12i).(2 + 3i)
= (-5.2 – 12.3) + (-5.3 + 12.2)i
= -46 + 9i
Lưu ý: Có thể tính (2 + 3i)3 bằng cách áp dụng hẳng đẳng thức
(2 + 3i)3 = 23 + 3.22.3i + 3.2.(3i)2 + (3i)3
= 8 + 36i + 54.(-1) + 27.(-1).i
= (8 – 54) + (36 – 27)i
= -46 + 9i
Trên đây là nội dung liên quan đến Cộng Trừ Và Nhân Số Phức – Toán 12 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!
