Để học tốt Đại 10, phần dưới giải các bài tập sách giáo khoa Toán 10 được biên soạn bám sát theo nội dung SGK Toán Đại Số 10. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Số Trung Bình Cộng. Số Trung Vị. Mốt – Toán 10 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
Lý thuyết Số trung bình cộng. Số trung vị. Mốt
Để thu được thông tin quan trọng từ các số liệu thống kê, người ta sử dụng những số đặc trưng như: số trung bình cộng, số trung vị, mốt, phương sai, dộ lệch chuẩn. Các số đạc trưng này phản ánh những khía cạnh khác nhau của dấu hiệu điều tra.
1. Số trung bình cộng : Kí hiệu: ![]()
Bảng phân bố tần suất và tần số
| Tên dữ liệu | Tần số | Tần suất (%) |
| x1
x2 . xk |
n1
n2 . nk |
f1
f2 . fk |
| Cộng | n = n1 + … + nk | 100% |
Trung bình cộng của các số liệu thống kê được tính theo công thức:
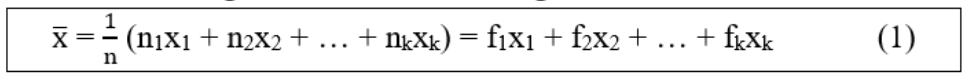
Trường hợp Bảng phân bố tần suất và tần số ghép lớp
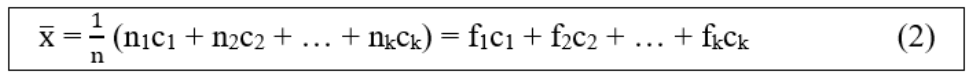
ci, fi, ni là giá trị đại diện của lớp thứ i.
Ý nghĩa của số trung bình:
Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đặc trưng quan trọng của mẫu số liệu.
Ví dụ 1: Một nhà thực vật học đo chiều dài của 74 chiếc lá cây và thu được số liệu sau ( đơn vị mm)
| Lớp | Giá trị đại diện | Tần số |
| [5,45 ; 5,85)
[5,85 ; 6,25) [6,25 ; 6,65) [6,65 ; 7,05) [7,05 ; 7,45) [7,45 ; 7,85) [7,85 ; 8,25) |
5,65
6,05 6,45 6,85 7,25 7,65 8,05 |
5
9 15 19 16 8 2 |
| N = 74 |
Khi đó chiều dài trung bình của 74 chiếc lá này là :
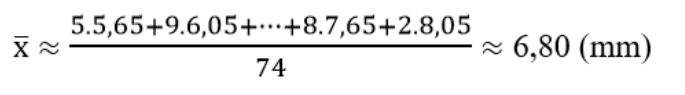
Ví dụ 2: Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp đến cao như sau: (thang điểm 100): 0 ; 0 ; 63 ; 65 ; 69 ; 70 ; 72 ; 78 ; 81 ; 85 ; 89.
Điểm trung bình là:
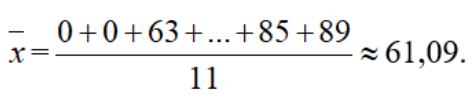
Quan sát dãy điểm trên, ta thấy hầu hết (9 em) trong nhóm có số điểm vượt điểm trung bình. Như vậy, điểm trung bình này không phản ứng đúng trình độ trung bình của nhóm.
2. Số trung vị:Kí hiệu: Me
Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.
Định nghĩa: Giả sử ta có dãy n số liệu được sắp xếp thành dãy không giảm (hoặc không tăng). Khi đó, số trung vị (của các số liệu thống kê đã cho) kí hiệu là Me là :
+ Số đứng giữa dãy nếu số phần tử N lẻ: ![]()
Trung bình cộng của hai số đứng giữa dãy nếu số phần tử N chẵn: 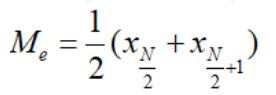
Ví dụ 1: Điểm thi toán của 9 học sinh như sau: 1; 1; 3; 6; 7; 8; 8; 9; 10
Ta có Me = 7
Ví dụ 2: Số điểm thi toán của 4 học sinh như sau: 1; 2,5; 8; 9,5
Ta có 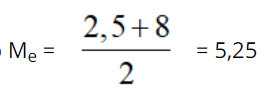
3. Mốt: Kí hiệu: Mo
Mốt của bảng phân bố tần số là giá trị (xi) có tần số (ni ) lớn nhất và được kí hiệu là Mo.
Chú ý: Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường hợp này có hai Mốt, kí hiệu Mo1,Mo2 .
Ví dụ :Một cửa hàng bán 6 loại quạt với giá tiền là 100, 150, 300, 350, 400, 500 (nghìn đồng). Số quạt cửa hàng bán ra trong mùa hè vừa qua được thống kê trong bảng tần số sau:
| Giá tiền | 100 | 150 | 300 | 350 | 400 | 500 |
| Số quạt bán được | 256 | 353 | 534 | 300 | 534 | 175 |
Mốt Mo = 300
4. Chọn đại diện cho các số liệu thống kê:
a) Trường hợp các số liệu thông kê cùng loại và số lượng thống kê đủ lớn (n ≥ 30) thì ta ưu tiên chọn số trung bình làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
b) Trường hợp không tính được giá trị trung bình thì ta chọn số trung vị hoặc mốt làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
c) Không nên dùng số trung bình để đại diện cho các số liệu thống kê trong các trường hợp sau (có thể dùng số trung vị hoặc mốt):
+ Số các số liệu thống kê quá ít (n ≤ 10).
+ Giữa các số liệu thống kê có sự chênh lệc quá lớn.
+ Đường gấp khúc tần suất không đối xứng, (và nhiều trường hợp khác)
Giải Bài Tập SGK
Bài 1 (trang 122 SGK Đại Số 10):
Tính số trung bình cộng của các bảng phân bố đã được lập ở các bài tập số 1 và số 2 của Bài 1.
Lời giải
Bài 1: Bảng phân bố tần số tuổi thọ của 30 bóng đèn điện.
| Tuổi thọ | Tần số |
| 1150 | 3 |
| 1160 | 6 |
| 1170 | 12 |
| 1180 | 6 |
| 1190 | 3 |
| Cộng | 30 |
Số trung bình:
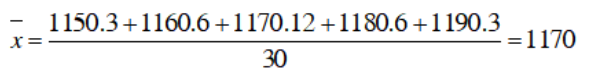
Bài 2: Bảng phân bố tần suất ghép lớp độ dài của 60 lá dương sỉ trưởng thành:
| Lớp của độ dài (cm) | Tần suất | Giá trị đại diện |
| [10; 20) | 13,3 | 15 |
| [20; 30) | 30,0 | 25 |
| [30; 40) | 40,0 | 35 |
| [40; 50) | 16,7 | 45 |
| Cộng | 100 (%) |
Số trung bình: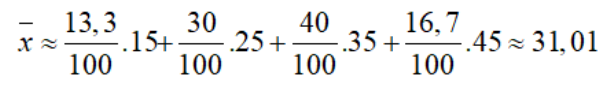
Bài 2 (trang 122 SGK Đại Số 10):
Trong một trường THPT, để tìm hiểu tình hình học môn Toán của hai lớp 10A, 10B, người ta cho hai lớp đó đồng thời làm bài thi môn toàn theo cùng một đề thi và lập được hai bảng phân bố tần số ghép lớp sau đây:
Điểm thi Toán của lớp 10A
| Lớp điểm thi | Tần số |
|---|---|
| [0; 2) | 2 |
| [2; 4) | 4 |
| [4; 6) | 12 |
| [6; 8) | 28 |
| [8; 10] | 4 |
| Cộng | 50 |
Điểm thi Toán của lớp 10B
| Lớp điểm thi | Tần số |
|---|---|
| [0; 2) | 4 |
| [2; 4) | 10 |
| [4; 6) | 18 |
| [6; 8) | 14 |
| [8; 10] | 5 |
| Cộng | 51 |
Hãy tính số trung bình cộng của hai bảng phân bố ở trên và nêu nhận xét về kết quả làm bài thi của hai lớp.
Lời giải

Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.
Bài 3 (trang 123 SGK Đại Số 10):
Điều tra tiền lương hàng tháng của 30 công nhân ở một xưởng may, ta có bảng phân bố tần số sau:
Tiền lương của 30 công nhân xưởng may
| Tiền lương(nghìn đồng) | Tần số |
|---|---|
| 300 | 3 |
| 500 | 5 |
| 700 | 6 |
| 800 | 5 |
| 900 | 6 |
| 100 | 5 |
| Cộng | 30 |
Tìm mốt của bảng phân bố trên. Nếu ý nghĩa của kết quả tìm được.
Lời giải
Trong bảng phân bố trên, hai giá trị 700 và 900 có cùng tần số lớn nhất là 6. Do đó ta có hai mốt là:
M0(1) = 700; M0(2) = 900.
Ý nghĩa:
+ Số công nhân có tiền lương 700.000đ/tháng và 900.000đ/tháng bằng nhau và chiếm đa số.
+ Tỉ lệ công nhân có mức lương 700 nghìn đồng / tháng và 900 nghìn đồng/ tháng cao hơn tỉ lệ công nhân có các mức lương khác.
Bài 4 (trang 123 SGK Đại Số 10):
Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch là: 650, 840, 690, 720, 2500, 3000 (đơn vị: nghìn đồng).
Tìm số trung vị của các số liệu đã thống kê đã cho. Nếu ý nghĩa của kết quả đã tính được.
Lời giải
Bảng số liệu có 7 giá trị, sắp các giá trị theo thứ tự không giảm ta có:
650, 670, 690, 720, 840, 2500, 3000.
Vì số phần tử = 7 là số lẻ nên số trung vị là Me = 720 (số chính giữa của dãy).
Ý nghĩa:
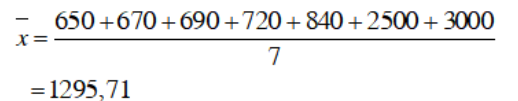
Số trung bình này chênh lệch quá lớn so với các số liệu nên không đại diện được cho các số liệu.
Trong trường hợp này, số trung vị nên được chọn làm giá trị đại diện cho mức lương.
Bài 5 (trang 123 SGK Đại Số 10):
Cho biết tình hình thu hoạch lúa vụ mùa năm 1980 của ba hợp tác xã ở địa phương V như sau:
| Hợp tác xã | Năng suất lúa(tạ/ha) | Diện tích trồng lúa(ha) |
|---|---|---|
| A | 40 | 150 |
| B | 38 | 130 |
| C | 36 | 120 |
Hãy tính năng suất lúa trung bình của vụ mùa năm 1980 trong toàn bộ ba hợp tác xã kể trên.
Lời giải
Ta biết sản lượng thu được = năng suất . diện tích.
Sản lượng lúa của HTX A là: 40.150 = 6000 (tạ)
Sản lượng lúa của HTX B là : 38.130 = 4940 (tạ)
Sản lượng lúa của HTX C là : 36.120 = 4320 (tạ)
Tổng sản lượng lúa của cả ba HTX là : 6000 + 4940 + 4320 = 15260 (tạ)
Tổng diện tích trồng của cả ba HTX là : 150 + 130 + 120 = 400 (ha)
Năng suất lúa trung bình của cả ba HTX : 15260 : 400 = 38,15 (tạ/ha)
*Lưu ý: Các bạn không thể tính năng suất trung bình bằng cách :
(40 + 38 + 36)/3 = 38 (tạ/ha)
vì khi chênh lệch diện tích lớn thì số trung bình càng không chính xác.
Trên đây là nội dung liên quan đến Số Trung Bình Cộng. Số Trung Vị. Mốt – Toán 10 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!




