Để học tốt Giải tích 12, phần này giúp bạn giải các bài tập trong sách giáo khoa Toán 12 được biên soạn bám sát theo nội dung sách Giải tích 12. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số – Toán 12 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
I. Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
A. Tóm tắt lý thuyết
Định nghĩa:
Cho hàm số y = f(x) xác định trên miền D
– Số M gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu: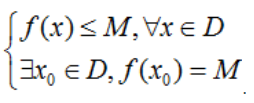 
.
Kí hiệu: 
– Số m gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu: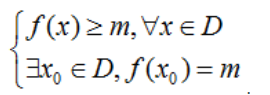 
.
Kí hiệu: 
B. Kĩ năng giải bài tập
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên K (K có thể là khoảng, đoạn, nửa khoảng, …)
1. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sử dụng bảng biến thiên
– Bước 1. Tính đạo hàm f'(x).
– Bước 2. Tìm các nghiệm của f'(x) và các điểm f'(x) trên K.
– Bước 3. Lập bảng biến thiên của f(x) trên K.
– Bước 4. Căn cứ vào bảng biến thiên kết luận 
2. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số không sử dụng bảng biến thiên
** Trường hợp 1. Tập K là đoạn [a; b]
– Bước 1. Tính đạo hàm f'(x) .
– Bước 2. Tìm tất cả các nghiệm xi ∈ [a; b] của phương trình f'(x) = 0 và tất cả các điểm α ∈ [a; b] làm cho f'(x) không xác định.
– Bước 3. Tính f(a), f(b), f(xi), f(αi).
– Bước 4. So sánh các giá trị tính được và kết luận 
.
** Trường hợp 2. Tập K là khoảng (a; b)
– Bước 1. Tính đạo hàm f'(x) .
– Bước 2. Tìm tất cả các nghiệm xi ∈ (a; b) của phương trình f'(x) = 0 và tất cả các điểm αi ∈ (a; b) làm cho f'(x) không xác định.
– Bước 3. Tính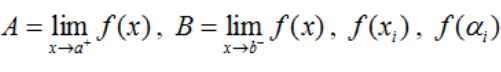 
.
– Bước 4. So sánh các giá trị tính được và kết luận 
.
** Chú ý: Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).
II. Giải Bài Tập SGK
Bài 1 (trang 23-24 SGK Giải tích 12):
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
a) y = x3 – 3x2 – 9x + 35 trên các đoạn [-4; 4] và [0; 5] ;
b) y = x4 – 3x2 + 2 trên các đoạn [0; 3] và [2; 5] ;
c)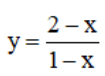 
trên các đoạn [2 ; 4] và [-3 ; -2] ;
d) 
trên đoạn [-1 ; 1].
Lời giải:
a) TXĐ: D = R.
y’ = 3x2 – 6x – 9;
y’ = 0 ⇔ x = –1 hoặc x = 3.
+ Xét hàm số trên đoạn [-4; 4] :
y(-4) = -41 ;
y(-1) = 40 ;
y(3) = 8
y(4) = 15.
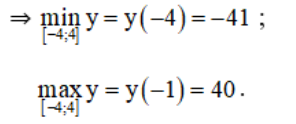
+ Xét hàm số trên [0 ; 5].
y(0) = 35 ;
y(3) = 8 ;
y(5) = 40.
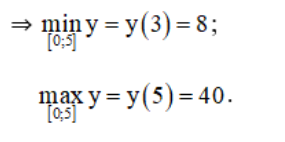
b) TXĐ: D = R
y’ = 4x3 – 6x
y’ = 0 ⇔ 2x.(2x2 – 3) = 0 ⇔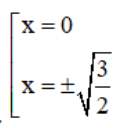 
+ Xét hàm số trên [0 ; 3] :
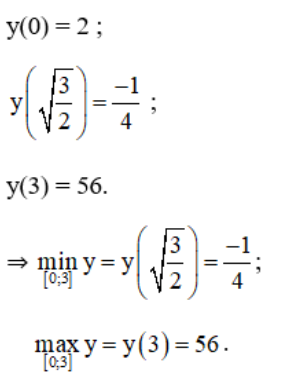
+ Xét hàm số trên [2; 5].
y(2) = 6;
y(5) = 552.
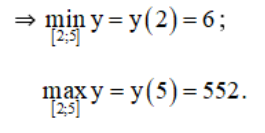
c) TXĐ: D = (-∞; 1) ∪ (1; +∞)
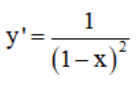> 0 với ∀ x ∈ D.
⇒ hàm số đồng biến trên (-∞; 1) và (1; +∞).
⇒ Hàm số đồng biến trên [2; 4] và [-3; -2]
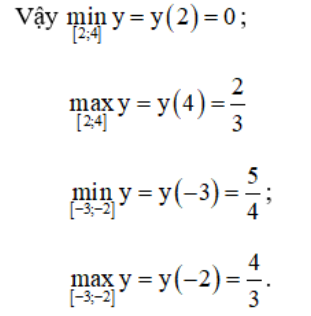
d) TXĐ: D = (-∞; 5/4]
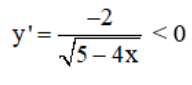với ∀ x ∈ (-∞; 5/4)
⇒ Hàm số nghịch biến trên (-∞; 5/4)
⇒ Hàm số nghịch biến trên [-1; 1]
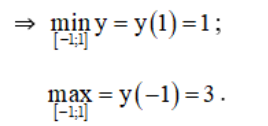
Bài 2 (trang 24 SGK Giải tích 12):
Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Lời giải:
Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.
Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)
⇒ độ dài cạnh còn lại là : 8 – x (cm)
⇒ Diện tích của hình chữ nhật là:
S = x(8 – x) = 8x – x2 = 16 – (16 – 8x + x2) = 16 – (x – 4)2 ≤ 16.
⇒ Smax = 16
Dấu bằng xảy ra khi (x – 4)2 = 0 ⇔ x = 4.
Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng 16cm2.
Bài 3 (trang 24 SGK Giải tích 12):
Trong tất cả các hình chữ nhật có diện tích 48 m2, hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Lời giải:
Gọi độ dài một cạnh của hình chữ nhật là x (m) (điều kiện: x > 0).
⇒ độ dài cạnh còn lại 
(m)
⇒ chu vi hình chữ nhật :
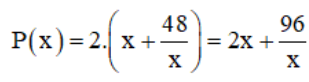
Xét hàm số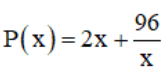 
trên (0; +∞):
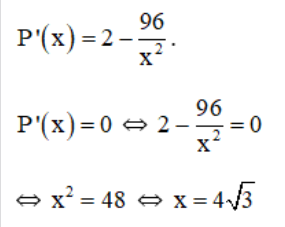
Bảng biến thiên trên (0; +∞):
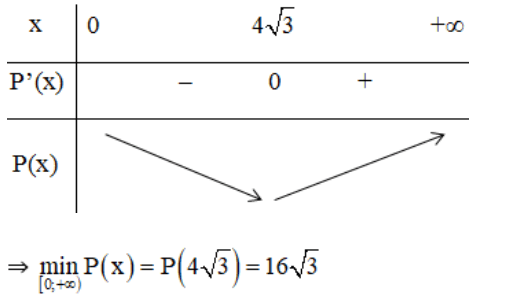
Vậy trong các hình chữ nhật có cùng diện tích 48m2 thì hình vuông cạnh 4√3 m có chu vi nhỏ nhất.
Bài 4 (trang 24 SGK Giải tích 12): Tính giá trị lớn nhất của các hàm số sau:
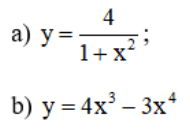
Lời giải:
a) TXĐ: D = R
Ta thấy: 1 + x2 ≥ 1
⇒ 
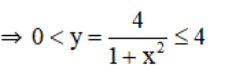
đạt được khi 1 + x2 = 1 ⇔ x = 0.
b) TXĐ : D = R
⇒ y’ = 12x2 – 12x3 = 12x2(1 – x)
y’ = 0 ⇔ x = 0 hoặc x = 1
Bảng biến thiên:
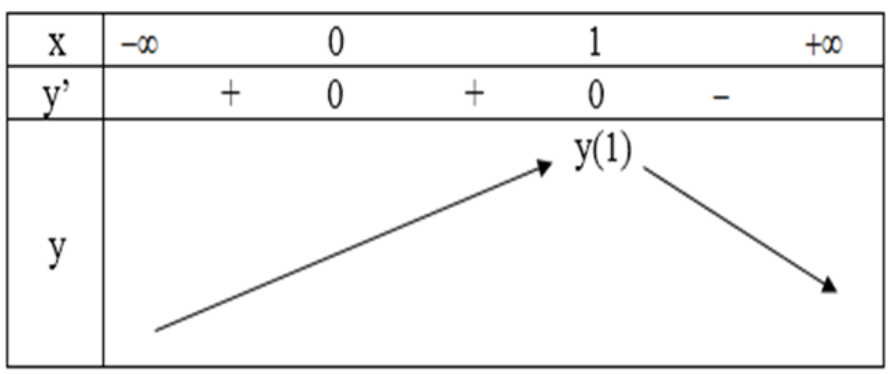
Từ bảng biến thiên suy ra: max y = y(1) = 1.
Bài 5 (trang 24 SGK Giải tích 12):
Tính giá trị nhỏ nhất của các hàm số sau:
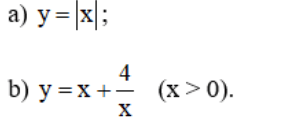
Lời giải:
a)
– Cách 1:
Ta có: y = |x| ≥ 0 ∀ x
⇒ Hàm số có giá trị nhỏ nhất là min y = 0 khi x = 0.
– Cách 2:
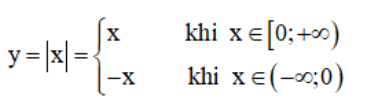
Bảng biến thiên:
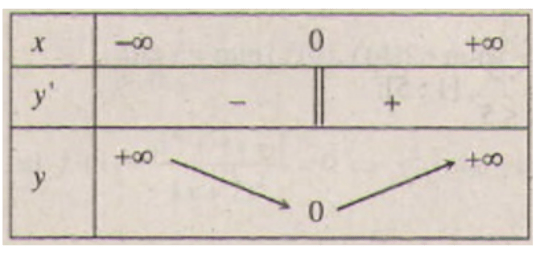
Từ bảng biến thiên suy ra: min y = 0
b) D = (0; +∞)
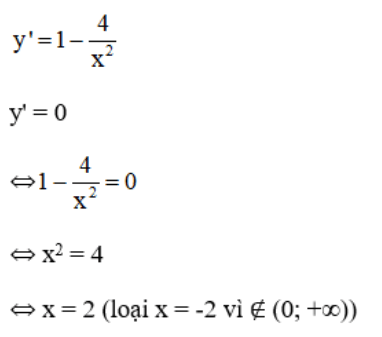
Bảng biến thiên:
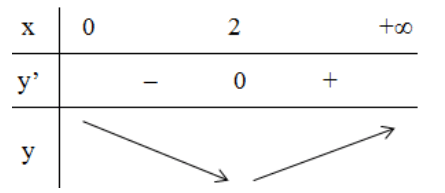
Từ bảng biến thiên suy ra: min y = y(2) = 4
Trên đây là nội dung liên quan đến Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số – Toán 12 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!
