Để học tốt Hình Học 10, phần dưới giải các bài tập sách giáo khoa Toán 10 được biên soạn bám sát theo nội dung SGK Toán Hình Học 10. Dưới đây chúng ta sẽ cùng tìm hiểu nội dung Giá Trị Lượng Giác Của Một Cung – Toán 10 và giải một số bài tập liên quan đến nội dung này để nắm chắc kiến thức nhé!
I. GIÁ TRỊ LƯỢNG GIÁC CỦA CUNG α
1. Định nghĩa
Trên đường tròn lượng giác cho cung 
có sđ = α (còn viết 
= α)
Tung độ y = 
của điểm M gọi là sin của α và kí hiệu là sinα
sin α =
Hoành độ x = 
của điểm M gọi là côsin của α và kí hiệu là cosα
cos α = 
Nếu cos α ≠ 0, tỉ số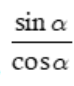 
gọi là tang của α và kí hiệu là tan α (người ta còn dùng kí hiệu tg α)
Tan α =
Nếu sinα ≠ 0 tỉ số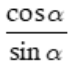 
gọi là côtang của α và kí hiệu là cotα (người ta còn dùng kí hiệu cotg α)
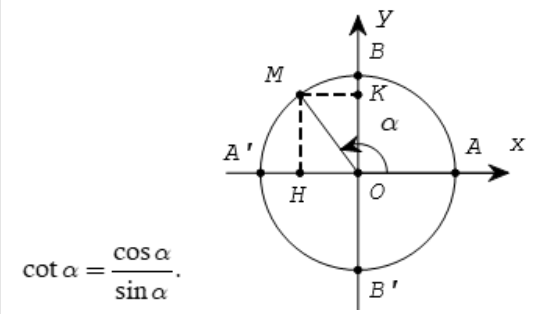Các giá trị sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của cung α. Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin
2. Hệ quả
1) sinα và cosα xác định với mọi α ∈ R. Hơn nữa, ta có
sin(α + k2π) = sin α, ∀k ∈ Z;
cos(α + k2π) = cos α, ∀k ∈ Z
2) Vì –1 ≤ ≤ 1; –1 ≤ ≤ 1 nên ta có
–1 ≤ sin α ≤ 1
–1 ≤ cos α ≤ 1
3) Với mọi m ∈ R mà –1 ≤ m ≤ 1 đều tồn tại α và β sao cho sin α = m và cos β = m.
4) tanα xác định với mọi α ≠ 
+ kπ (k ∈ Z)
5) cotα xác định với mọi α ≠ kπ (k ∈ Z)
6) Dấu của các giá trị lượng giác của góc α phụ thuộc vào vị trí điểm cuối của cung = α trên đường tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
| Giá trị lượng giác |Góc phần tư | I | II | III | IV |
| cos α | + | – | – | + |
| sin α | + | + | – | – |
| tan α | + | – | + | – |
| cot α | + | – | + | – |
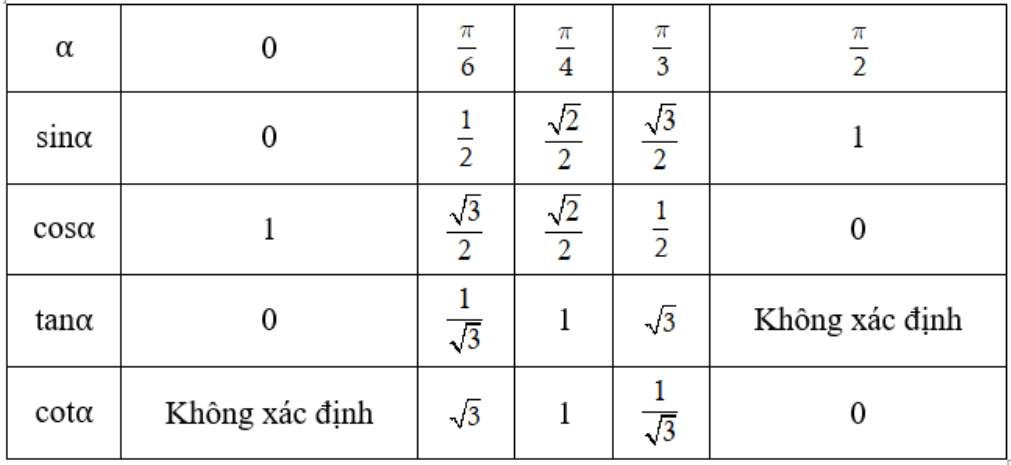
3. Giá trị lượng giác của các cung đặc biệt
II. Ý NGHĨA HÌNH HỌC CỦA TANG VÀ CÔTANG
1. Ý nghĩa hình học của tan α
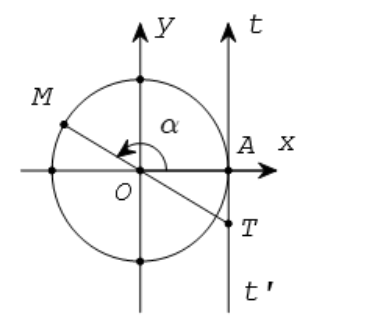
Từ A vẽ tiếp tuyến t’At với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại A.
Gọi T là giao điểm của OM với trục t’At.
tanα được biểu diễn bởi độ dài đại số của vectơ 
trên trục t’At. Trục t’At được gọi là trục tang.
2. Ý nghĩa hình học của cot α
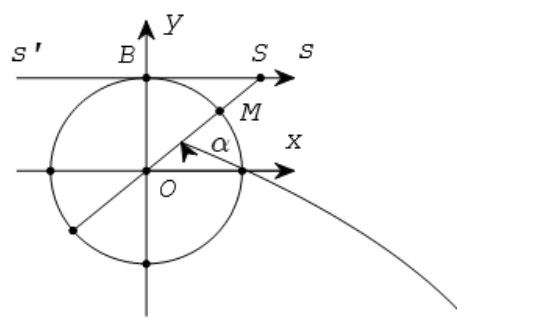
Từ B vẽ tiếp tuyến s’Bs với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại B.
Gọi S là giao điểm của OM với trục s’Bs
cot α được biểu diển bởi độ dài đại số của vectơ 
trên trục s’Bs. Trục s’Bs được gọi là trục côtang.
III – QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC
1. Công thức lượng giác cơ bản
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau
sin2α + cos2α = 1
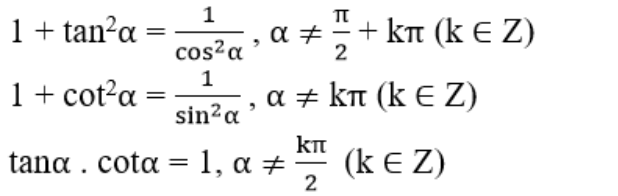
2. Giá trị lượng giác của các cung có liên quan đặc biệt
1) Cung đối nhau: α và –α
cos(-α) = cosα
sin(-α) = –sinα
tan(-α) = –tanα
cot(-α) = –cotα
2) Cung bù nhau: α và π-α
sin(π-α) = sinα
cos(π-α) = –cosα
tan(π-α) = –tanα
cot(π-α) = –cotα
3) Cung hơn kém π : α và (α + π)
sin(α + π) = –sinα
cos(α + π) = –cosα
tan(α + π) = tanα
cot(α + π) = cotα
4) Cung phụ nhau: α và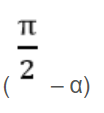 
sin = cosα
cos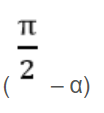 = sinα
tan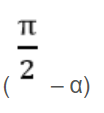) = cotα
cot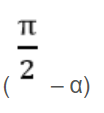 = tanα
IV. GIẢI BÀI TẬP SGK
Bài 1 (trang 148 SGK Đại Số 10):
Có cung α nào mà sinα nhận các giá trị tương ứng sau đây không ?
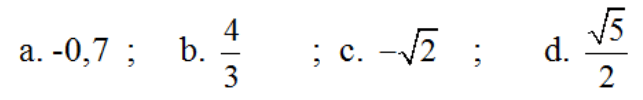
Lời giải
Ta có: -1 ≤ sin α ≤ 1 với mọi α ∈ R.
a) Vì -1 < –0,7 < 1 nên tồn tại cung α thỏa mãn sin α = -0,7.
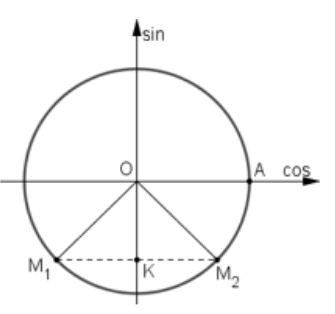
Trên trục tung xác định điểm K sao cho 
Từ K kẻ đường thẳng vuông góc với trục tung cắt đường tròn lượng giác tại hai điểm M1 và M2.
Khi đó với 
thì theo định nghĩa sin α = 
b) Vì 4/3 > 1 nên không tồn tại α để sin α = 4/3.
c) Vì -√2 < -1 nên không tồn tại α để sin α = -√2.
d) Vì √5/2 > 1 nên không tồn tại α để sin α = √5/2
Bài 2 (trang 148 SGK Đại Số 10):
Các đẳng thức sau đây có thể đồng thời xảy ra không ?
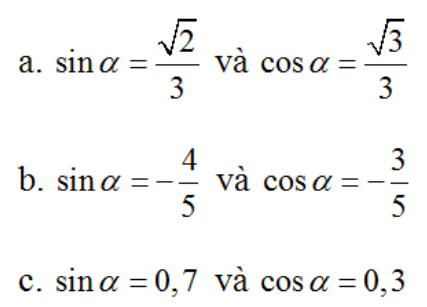
Lời giải
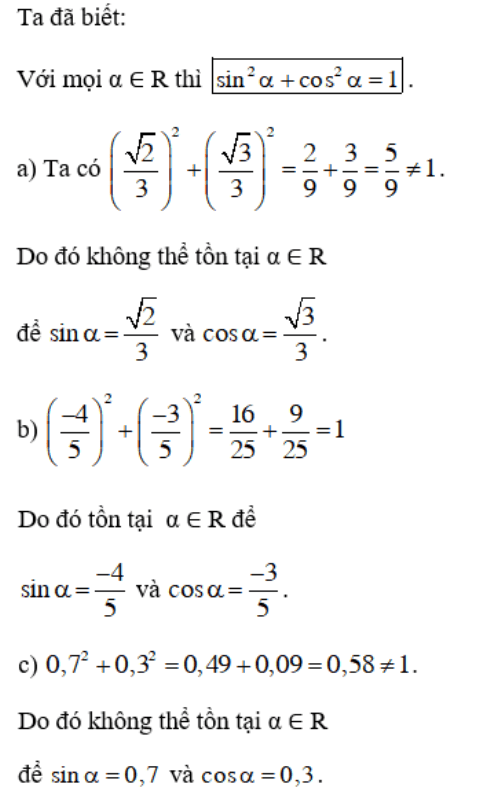
Bài 3 (trang 148 SGK Đại Số 10):
Cho 0 < α < π/2. Xác định dấu của các giá trị lượng giác
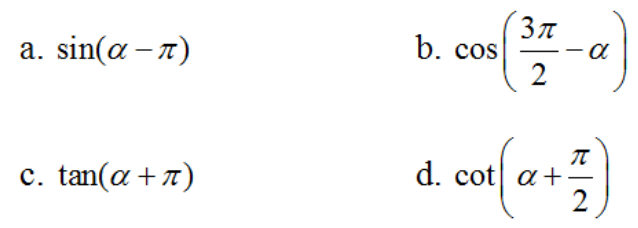
Lời giải
Vì 0 < α < π/2 nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.
Cách 1: Dựa vào mối quan hệ giữa các giá trị lượng giác của các cung có liên quan đặc biệt
a) sin (α – π) = – sin (π – α) (Áp dụng công thức sin (- α) = – sin α)
= -sin α (Áp dụng công thức sin (π – α) = sin α)
Mà sin α > 0 nên sin (α – π) < 0.
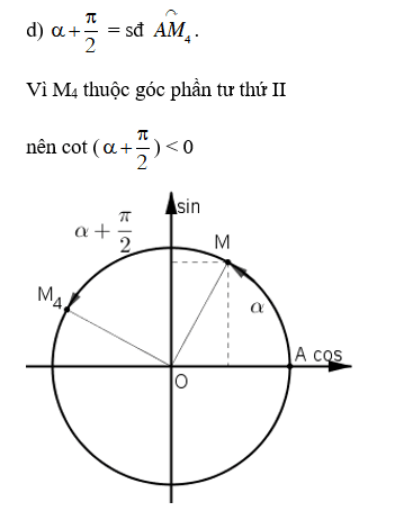
c) tan (α + π) = tan α.
Mà tan α > 0 nên tan (α + π) > 0.
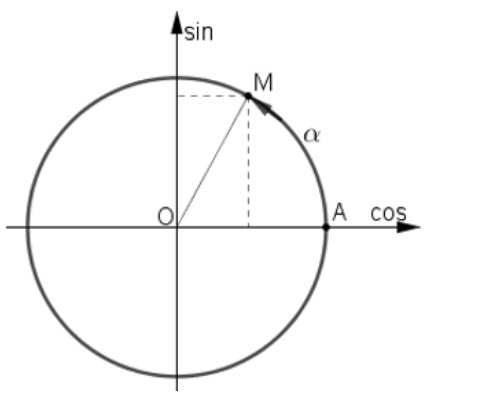
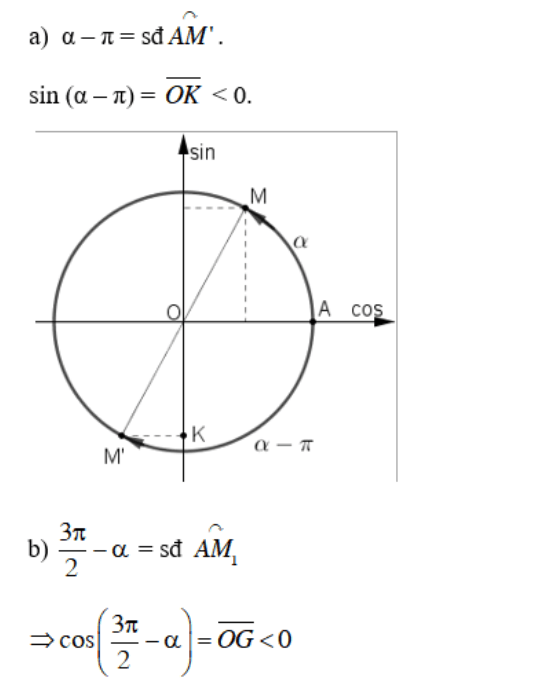
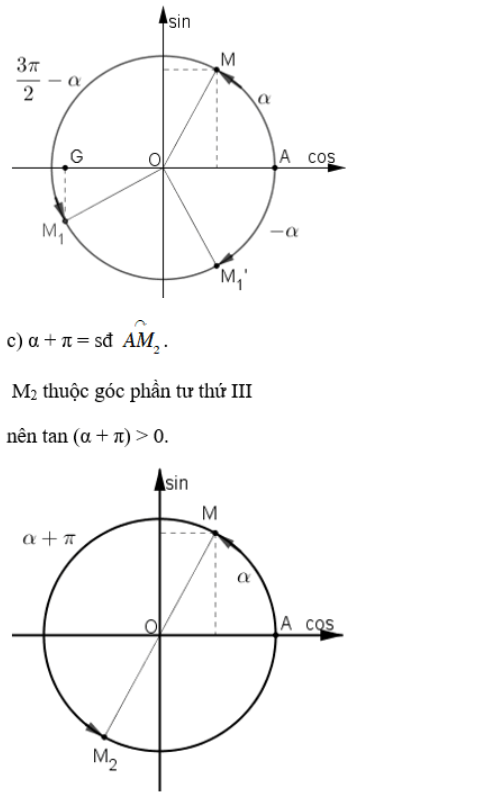
Cách 2: Dựa vào biểu diễn cung trên đường tròn lượng giác:
Vì 0 < α < π/2 nên ta biểu diễn α = sđ 
như trên hình vẽ.
Bài 4 (trang 148 SGK Đại Số 10):
Tính các giá trị lượng giác của góc α nếu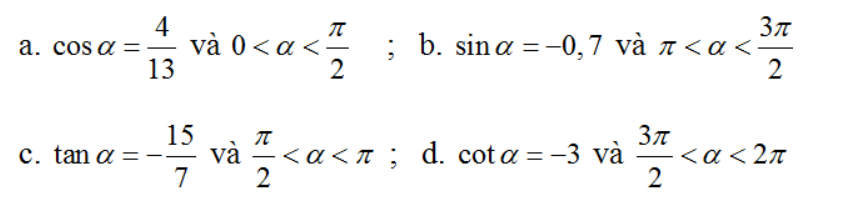
Lời giải
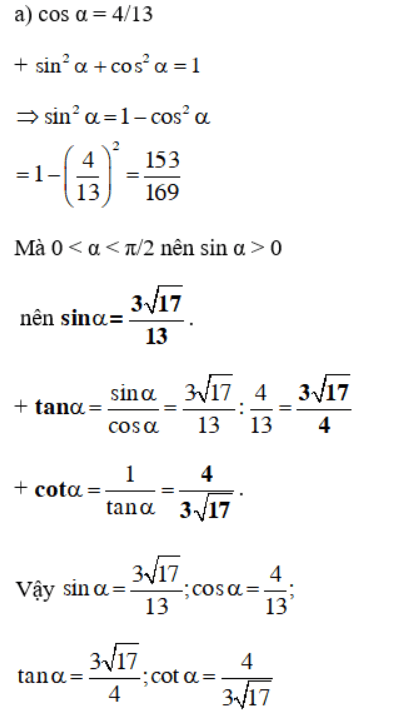
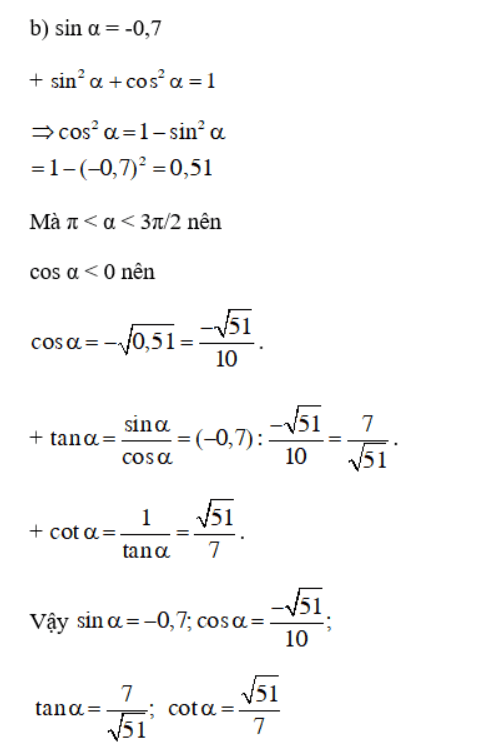
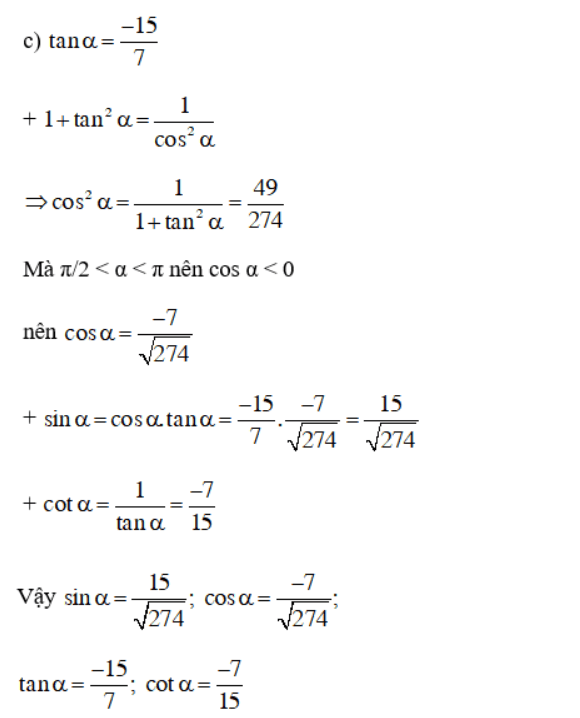
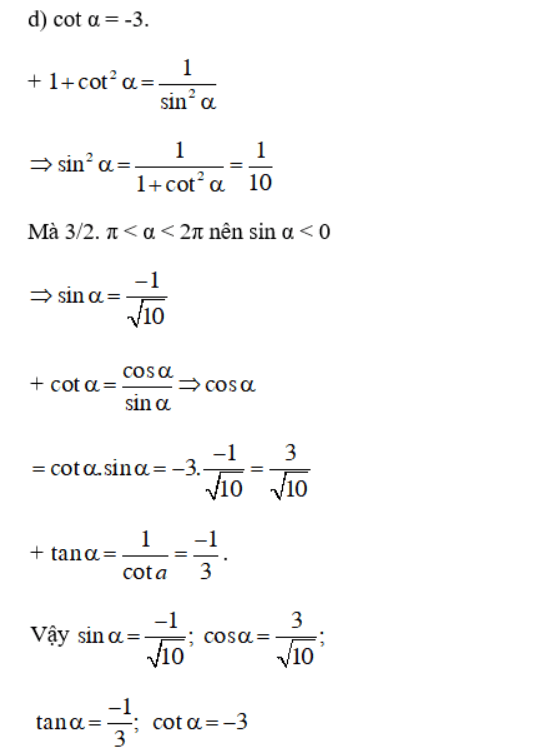
Bài 5 (trang 148 SGK Đại Số 10):
Tính α, biết
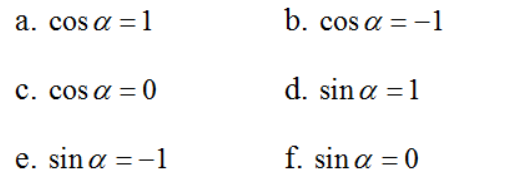
Lời giải
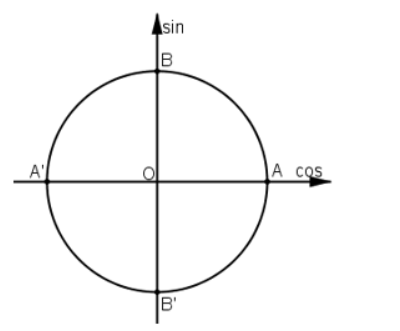
a) cos α = 1 ⇔ M trùng với A hay α = k.2π, k ∈ Z.
b) cos α = -1 ⇔ M trùng với A’ hay α = π + k.2π, k ∈ Z
c) cos α = 0 ⇔ M trùng với B hoặc B’ hay α = π/2 + k.π, k ∈ Z
d) sin α = 1 ⇔ M trùng với B hay α = π/2 + k.2π, k ∈ Z
e) sin α = -1 ⇔ M trùng với B’ hay α = -π/2 + k.2π, k ∈ Z
f) sin α = 0 ⇔ M trùng với A hoặc A’ hay α = k.π, k ∈ Z
Trên đây là nội dung liên quan đến Giá Trị Lượng Giác Của Một Cung – Toán 10 được dean2020.edu.vn đã tổng hợp được và chia sẻ đến các bạn. Hy vọng những kiến thức mà chúng tôi chia sẻ sẽ mang lại cho bạn những thông tin bổ ích nhé!
